Let PQR be a triangle of area with a=2,b=72,andc=52,wherea,b,andc are the lengths of the sides of the triangle opposite to the angles at P,Q,andR respectively. Then 2sinP−sin2P2sinP+sin2Pequals 34 (b) 454 (c) (34)2 (d) (454)2Solution in Tamil
34Δ
454Δ
(34Δ)2
(454Δ)5
The correct Answer is:C
If ΔABC has sides a,b,c,
Then tan(A/2)=√(s−b)(s−a)s(s−a)
Where s=a+b+c2
⇒s=2+72+522=4
∴2sinP−sin2P2sinP+sin2P=2sinP(1−cosP)2sinP(1+cosP)
=2sin2(P/2)2cos2(P/2)=tan2(P/2)
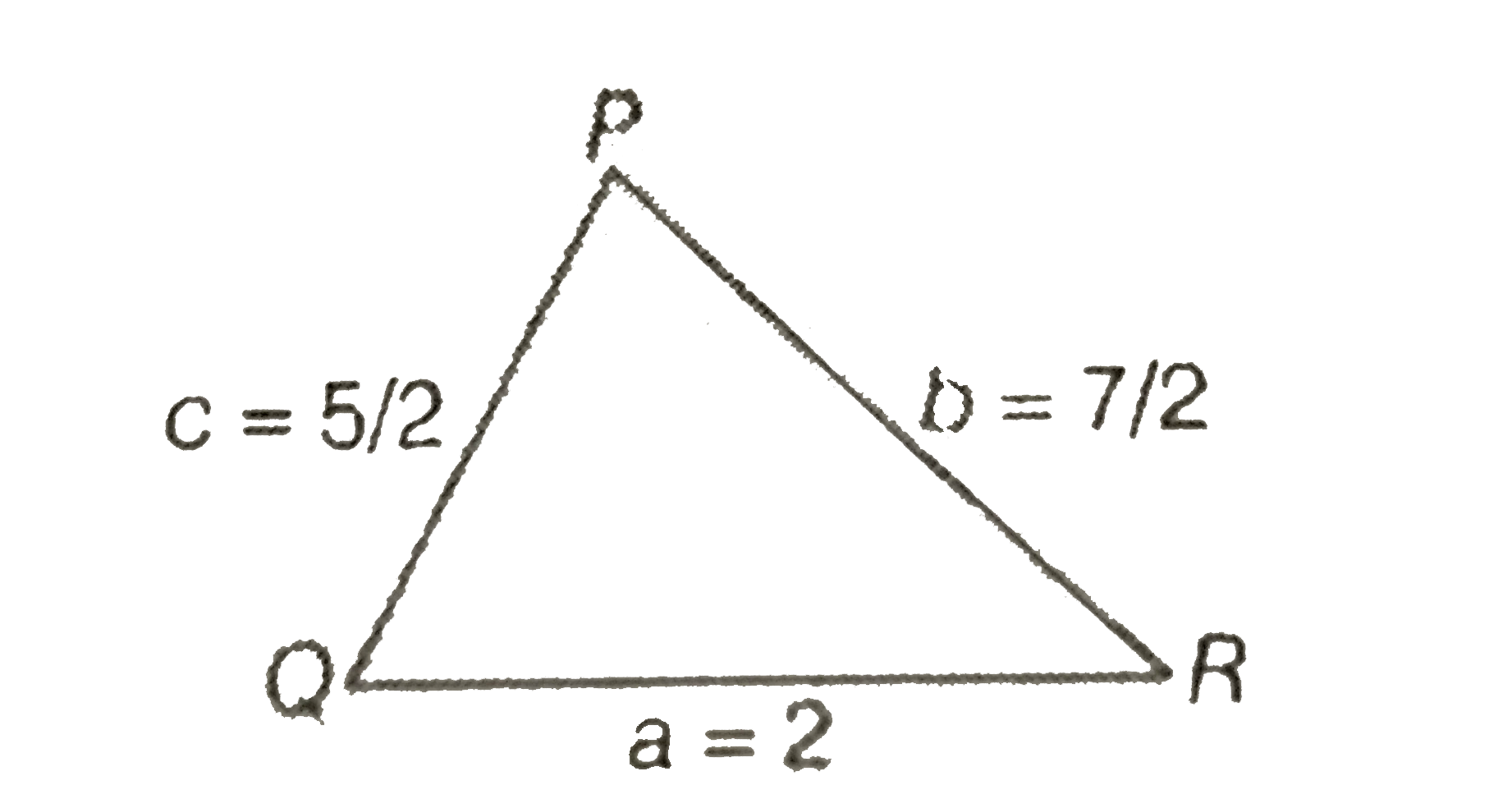
(s−b)(s−c)s(s−a)×(s−b)(s−c)(s−b)(s−c)
=[(s−b)2(s−c)2]Δ2(4−72)2(4−52)2Δ2=(34Δ)2
Similar Questions
If a,b,andc are in A.P. p,q,andr are in H.P., and ap,bq,andcr are in G.P., then pr+rp is equal to ac−ca b. ac+ca c. bq+qb d. bq−qb
View Solutionएक त्रिभुज PQR का क्षेत्रफ़ल Δ है और a=2,b=72 और c=52 है जहाँ a,b और c क्रमशः कोण P,Q और R के सम्मुख भुजाओं की लम्बाईयाँ है तो 2sinP−sin2P2sinP+sin2P का मान बराबर है
View SolutionLet PQR be a triangle of area Δ with a=2,b=72andc=52,
where a,bandc are the lengths of the sides of the triangle opposite to the angles at
P,QandR respectively. Then 2sinP−sin2P2sinP+sin2P equals
View SolutionLet POR be a triangle of area Δ with a=2,b=72andc=52 here a, b and c are the lengths of the sides of the triangle opposite to the angles at P, Q and R respectively. Then 2sinP−sin2P2sinP+sin2P equals
View SolutionLet PQR be a triangle of area Δ with a=2,b=72andc=52, where a,b and c are the lengths of the sides of the triangle opposite to the angles at P,Q and R respectively. Then (2sinP−sin2P2sinP+sin2P) equals
View SolutionLet H:x2a2−y2b2=1 , where a>b>0 , be a hyperbola in the xy -plane whose conjugate axis LM subtends an angle of 60o at one of its vertices N . Let the area of the triangle LMN be 4√3 . LIST-I LIST-II P. The length of the conjugate axis of H is 1. 8 Q. The eccentricity of H is 2. √43 R. The distance between the foci of H is 3. 2√3 S. The length of the latus rectum of H is 4. 4 The correct option is P→4; Q→2; R→1; S→3 (b) P→4; Q→3; R→1; S→2 (c) P→4; Q→1; R→3; S→2 (d) P→3; Q→4; R→2; S→1
View SolutionIn triangle ABC, if cosA+cosB+cosC=74,thenRr is equal to 34 (b) 43 (c) 23 (d) 32
View SolutionLet P Q R be a triangle of area with a=2,b=7/2,a n dc=5/2, w h e r ea , b ,a n dc are the lengths of the sides of the triangle opposite to the angles at P ,Q ,a n dR respectively. Then (2sinP-sin2P)/(2sinP+sin2P)e q u a l s
View Solution
