If the anlges of elevation of the top of a tower from three collinear points A,B and C on a line leading to the foot of the tower are $30^{\circ}, 45^{\circ} and 60^{\circ}$ respectively , then the ratio AB:BC is Solution in Tamil

A

$\sqrt{3} : 1$

B

$\sqrt{3} : \sqrt{2}$

C

$1 : \sqrt{3}$

D

$2 : 3$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

According to the given information, the figure should be as follows:
Let the height of tower $= h$
In $△ E D A, {tan 30}^{\circ} = \frac{E D}{A D}$
$\frac{1}{\sqrt{3}} = \frac{E D}{A D} = \frac{h}{A D}$
$\Rightarrow A D = h \sqrt{3}$

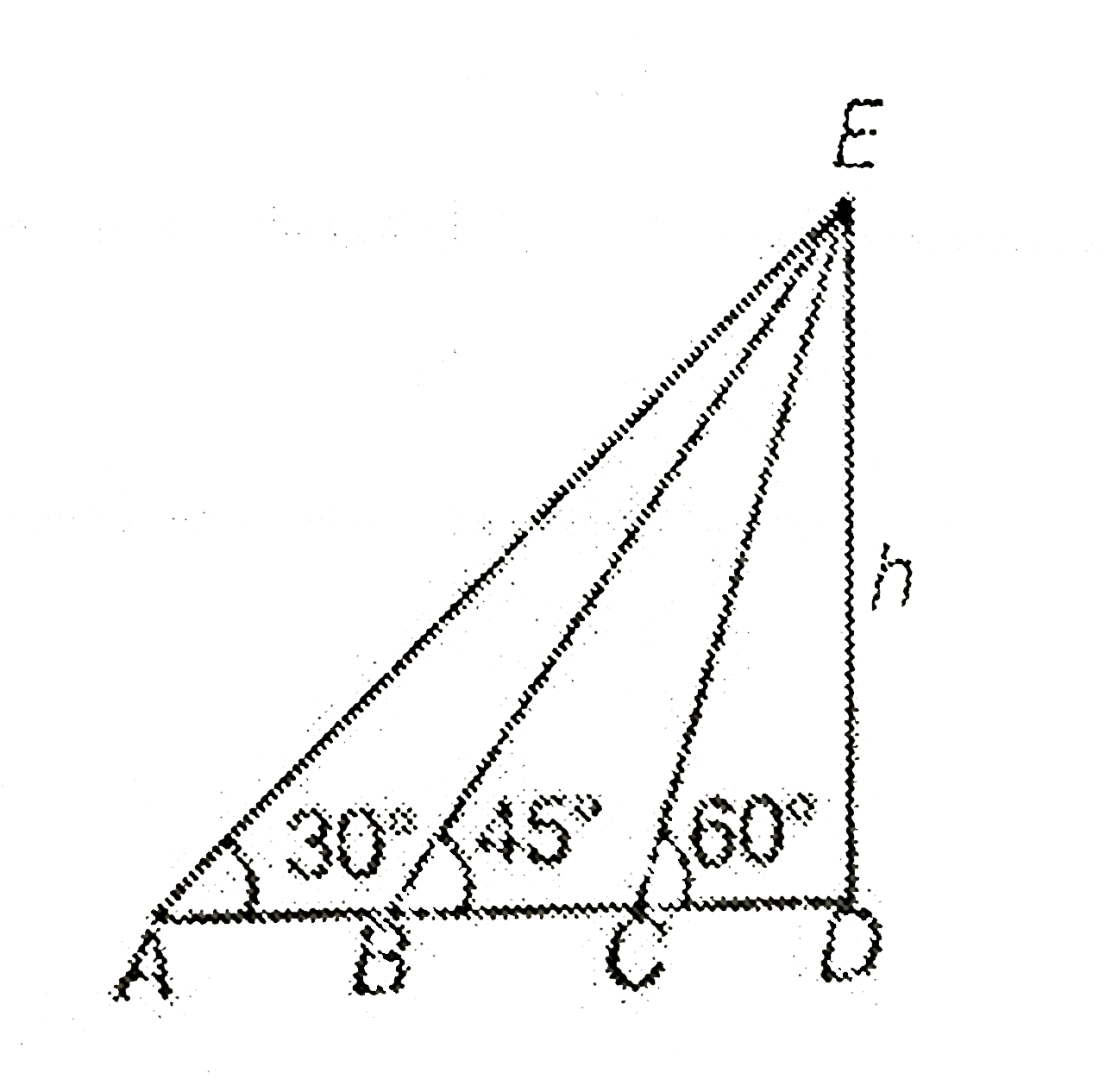
In $△ E D B, {tan 45}^{\circ} = \frac{h}{B D} \Rightarrow B D = h$
In $△ E D C, {tan 60}^{\circ} = \frac{h}{C D} \Rightarrow C D = \frac{h}{\sqrt{3}}$
Now, $\frac{A B}{B C} = \frac{A D - B D}{B D - C D} \Rightarrow \frac{A B}{B C} = \frac{h \sqrt{3} - h}{h - \frac{h}{\sqrt{3}}}$
$\Rightarrow \frac{A B}{B C} = \frac{h (\sqrt{3} - 1)}{\frac{h (\sqrt{3} - 1)}{\sqrt{3}}} \Rightarrow \frac{A B}{B C} = \frac{\sqrt{3} - 1}{(\sqrt{3} - 1)} \times \sqrt{3}$
$\Rightarrow \frac{A B}{B C} = \frac{\sqrt{3}}{1} ∴ A B : B C = \sqrt{3} : 1$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile