A cylindrica container is to be made from certain solid material with the following constraints: It has a fixed inner volume of Vmm3, has a 2 mm thick solid wall and is open at the top. The bottom of the container is a solid circular disc of thickness 2mm and is of radius equal to the outer radius of the container. If the volume the material used to make the container is minimum when the inner radius of the container is 10mm. then the value of V250π isSolution in Tamil
The correct Answer is:4
Here, volume of cylindrical container, V=πr2h … (i)
and let volume of the meterical used be T.
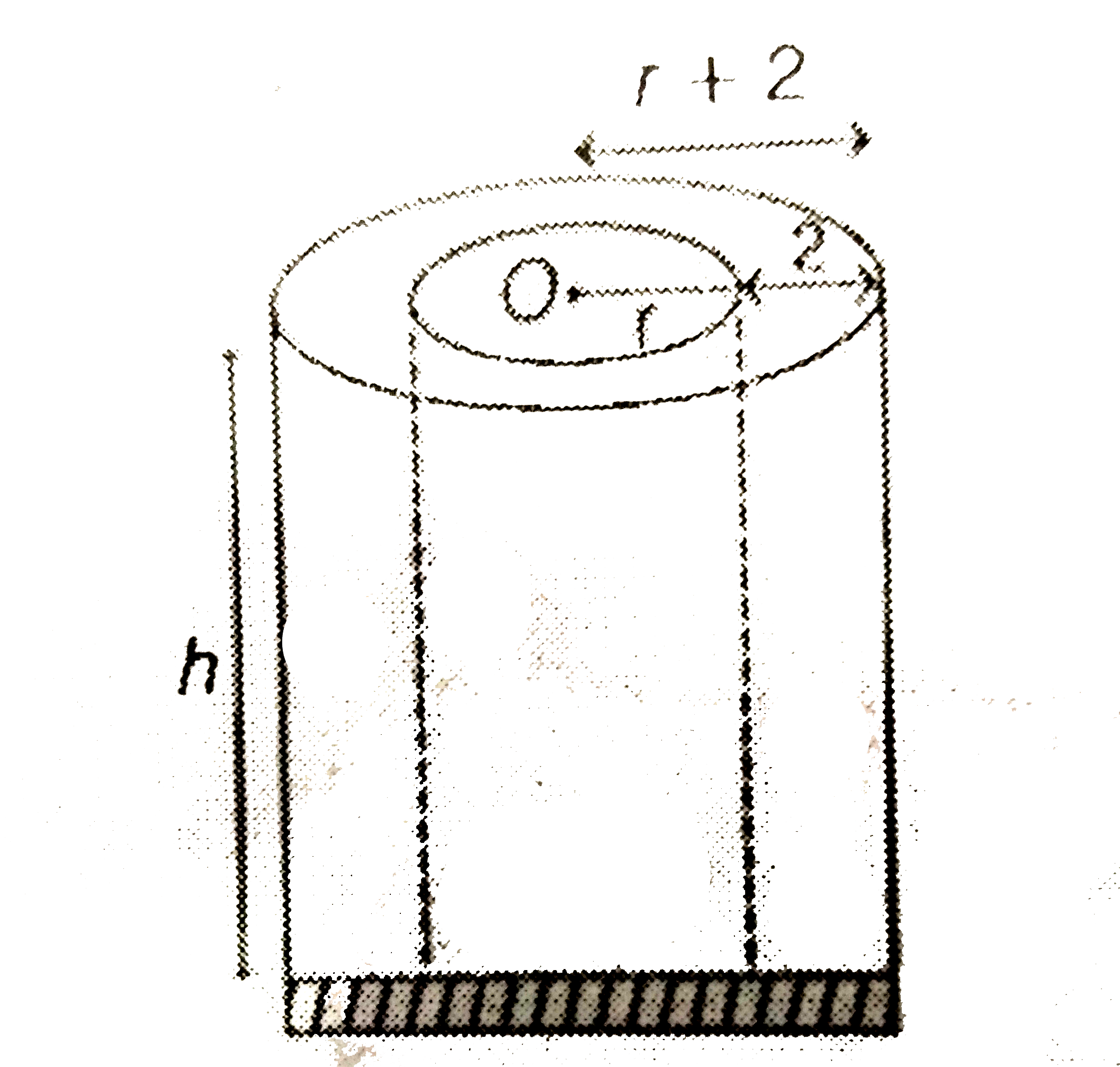
∴ T=π[(r+2)2−r2]h+π(r+2)2×2
⇒ T=π[(r+2)2−r2]⋅Vπr2+2π(r+2)2
[∵V=πr2h⇒h=Vπr2]
⇒T=V(r+2r)2+2π(r+2)2−V
On differentiating w.r.t. r, we get
dTdr=2V⋅(r+2r)⋅(−2r2)+4π(r+2)
At r=10,dTdr=0
Now, 0(r+2)⋅4(π−Vr3)
⇒ Vr3=π
where r=10
⇒ V1000=π
or V250π=4
Similar Questions
निम्न व्यवरोधों को संतुष्ट करते हुये एक बेलनाकार पात्र एक ठोस पदार्थ से बनाया है : पात्र का आंतरिक आयतन v घन मिमी नियत है तथा इसकी दीवारें 2 मिमी मोटाई की हैं एवं पात्र ऊपर से खुला हुआ है। पात्र का निचला तल 2 मिमी मोटाई वाला ठोस वृत्तीय डिस्क है तथा जिसकी त्रिज्या , पात्र की बाहरी त्रिज्या के बराबर है। यदि पात्र की आंतरिक त्रिज्या 10 मिमी होने पर पदार्थ के न्यूनतम आयतन की आवश्यकता होती हो, तब V250π का मान ज्ञात करो ।
View SolutionRadioactive materials are kept in thick-walled _______ containers.
View SolutionA cylindrical container is to be made from certain solid material with the following constraints: It has a fixed inner volume of Vm3, has a 2 mm thick solid wall and is open at the top. The bottom of the container is a solid circular disc of thickness 2mm and is of radius equal to the outer radius of the container. If the volume the material used to make the container is minimum when the inner radius of the container is 10mm. then the value of V250π is
View Solutionनिम्न व्यवरोधों को संतुष्ट करते हुए एक बेलनाकार पात्र एक ठोस पदार्थ से बनाया है : पात्र का आंतरिक आयतन V घन मिमी नियत है तथा इसकी दीवारें 2 मिमी मोटाई की है एवं पात्र ऊपर से खुला है। पात्र का निचला तल 2 मोटाई वाला ठोस वृत्तीय डिस्क है तथा जिसकी त्रिज्या , पात्र की बाहरी त्रिज्या के बराबर है। यदि पात्र की आंतरिक त्रिज्या 10 मिमी होने पर पदार्थ के न्यूनतम आयतन की आवश्यकता होती हो , तब V250π का मान है
View Solutionनिम्न व्यवरोधों को संतुष्ट करते हुये एक बेलनाकार पात्र एक ठोस पदार्थ से बनाया है : पात्र का आंतरिक आयतन v घन मिमी नियत है तथा इसकी दीवारें 2 मिमी मोटाई की हैं एवं पात्र ऊपर से खुला हुआ है। पात्र का निचला तल 2 मिमी मोटाई वाला ठोस वृत्तीय डिस्क है तथा जिसकी त्रिज्या , पात्र की बाहरी त्रिज्या के बराबर है। यदि पात्र की आंतरिक त्रिज्या 10 मिमी होने पर पदार्थ के न्यूनतम आयतन की आवश्यकता होती हो, तब V250π का मान ज्ञात करो ।
View Solution4 सेमी त्रिज्या वाले 16 सेमी ऊँचे एक लोहे के ठोस बेलन से 2 मिमी त्रिज्या की ठोस गोलियाँ बनाई जा सकती हैं
View SolutionA cylindrical container is to be made from certain solid material which the following constraints : It has a fixed inner volume of Vmm3, has a 2 mm thick solid wall and is open at the top. The bottom of the container is a solid circular disc of thickness 2 mm and is of radius equal to the outer radius of the container.
If the volume of the materia! used to make the container is minimum when the inner radius of the container is 10 mm, then the value of V250π is
View SolutionA cylindrica container is to be made from certain solid material with the following constraints: It has a fixed inner volume of V mm^3 , has a 2 mm thick solid wall and is open at the top. The bottom of the container is a solid circular disc of thickness 2mm and is of radius equal to the outer radius of the container. If the volume the material used to make the container is minimum when the inner radius of the container is 10 mm . then the value of V/(250 pi) is
View Solution