The function f(x)=∫x−1t(et−1)(t−1)(t−2)3(t−3)5dt has a local minimum at x= 0 (b) 1 (c) 2 (d) 3Solution in Tamil
0
1
2
3
The correct Answer is:B, D
f(x)=∫x−1t(et−1)(t−1)(t−2)3(t−3)5dt

f'(x)=ddx∫x−1t(et−1)(t−1)(t−2)3(t−3)5dt
=x(ex−1)(x−1)(x−2)3(x−3)5×1
[∵ddx∫ψ(x)ϕ(x)f(t)dt=f{ψ(x)}ψ'(x)−f(ϕ(x)}ϕ'(x)]
For local minimum, f'(x)=0
⇒ x=0,1,2,3
Let f'(x)=g(x)=x(ex−1)(x−1)(x−2)3(x−3)5
Using sign rule,
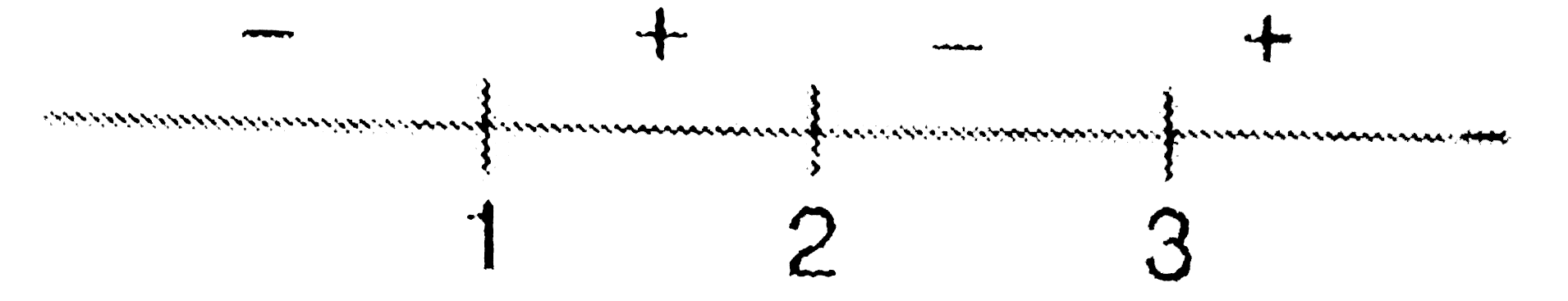
This shows that f(x) has a local minimum at x=1andx=3 and maximum at x=2
Therefore, (b) and (d) are the correct answers.
Similar Questions
Then function f(x)=∫x−2t(et−1)(t−2)3(t−3)5dt has a local minima at x=
View SolutionThe function f(x)=int_(-1)^(x)t(e^(t)-1)(t-1)(t-2)^(3)(t-3)^(5) dt has a local minimum at x=
View SolutionThe function f(x)=x∫−1t(et−1)(t−1)(t−2)3(t−3)5 dt has a local maximum at x =
View SolutionThe function f(x)=x∫−1t(et−1)(t−1)(t−2)3(t−3)5 dt has a local minimum at 'x' equal to
View Solutionif f(x)=∫x−1t(et−1)(t−1)(t−2)3(t−3)5dthas a local minimum then sum of values of x
View Solution(i) If f(x)=∫sin2x0sin−1√tdt+∫cos2x0cos−1√t dt, then prove that f'(x)=0∀x∈R.
(ii) Find the value of x for which function f(x)=∫x−1t(et−1)(t−1)(t−2)3(t−3)5dt has a local minimum.
View SolutionThe function ∫x−1t(et−1)(t−1)(t−2)3(t−3)5dt has local minimum at x=
View SolutionIf f(x) = ∫et^2(t - 2)(t - 3)dt for t ∈ [0, x] for x ∈ (0, ∞), then (A) f has a local maximum at x = 2 (B) f is decreasing on (2, 3) (C) there exists some c∈(0, ∞) such that f′′(c) = 0 (D) f has a local minimum at x = 3.
View Solution