Let f(x)=∫ex(x−1)(x−2)dx. Then f decreases in the interval (−∞,−2) (b) −2,−1) (1,2) (d) (2,+∞)Solution in Tamil
(−∞,−2)
(−2,−1)
(1,2)
(2,∞)
The correct Answer is:B
Let f(x)=∫ex(x−1)(x−2)dx
⇒ f'(x)=ex(x−1)(x−2)
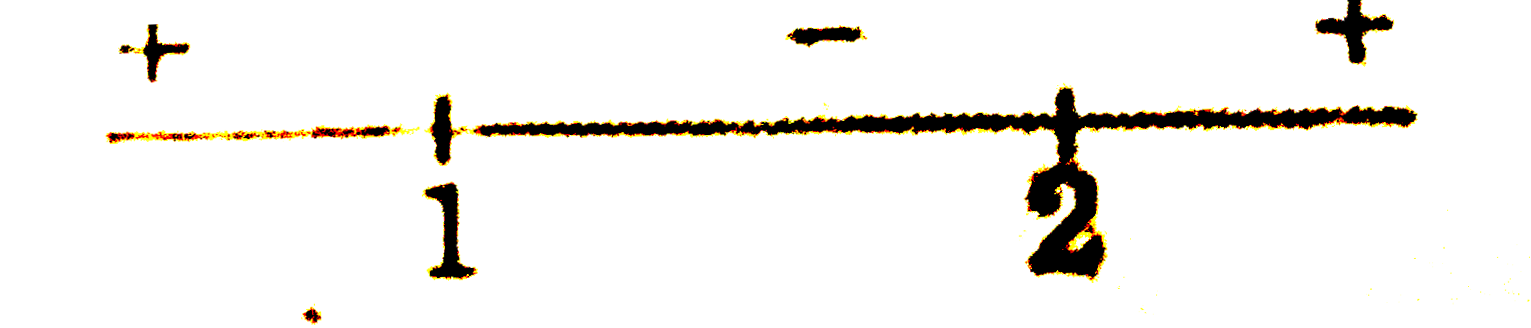
∴f'(x)<0 for 1<x<2
⇒f(x) is decreasing for x∈(1,2).
Similar Questions
Let f:(−∞,1]→(−∞,1] such that f(x)=x(2−x), then f−1(x) is :
View SolutionLet f be the function f(x)=cosx−(1−x22). Then (a) f(x) is an increasing function in (0,∞) (b) f(x) is a decreasing function in (−∞,∞) (c) f(x) is an increasing function in (−∞,∞) (d) f(x) is a decreasing function in (−∞,0)
View SolutionShow that f(x)=11+x2 decreases in the interval [0,∞) and increases in the interval (−∞,0].
View SolutionShow that f(x)=11+x2 decreases in the interval [0, ∞) and increases in the interval (−∞, 0] .
View SolutionLet f(x)=∫ex(x−1)(x−2)dx. Then f decreases in the interval a)(−∞,−2) (b) −2,−1) (1,2) (d) (2,+∞)
View SolutionLet f(x)=∫x3x2dtlnt for x>1andg(x)=∫x1(2t2−lnt)f(t)dt(x>1), then: (a) g is increasing on (1,∞) (b) g is decreasing on (1,∞) (c) g is increasing on (1,2) and decreasing on (2,∞) (d) g is decreasing on (1,2) and increasing on (2,∞)
View SolutionLet f be the function f(x)=cosx−(1−x22). Then f(x) is an increasing function in (0,∞) f(x) is a decreasing function in (−∞,∞) f(x) is an increasing function in (−∞,∞) f(x) is a decreasing function in (−∞,0)
View SolutionLet f(x)=∫ex(x−1)(x−2)dx. Then f decreases in the interval (a)(−∞,−2) (b) −2,−1) (c)(1,2) (d) (2,+∞)
View Solution