Let the functions defined in Column I (1+2x) , tan xhave domain (−π2,π2) and range (−∞,∞) Solution in Tamil
The correct Answer is:A→q;B→r
y=1+2x is linear function, therefore it is one-one and its range is (−π+1,π+1). Therefore (1 + 2x) is one-one but not onto so (A)→(q). Again, see the figure.
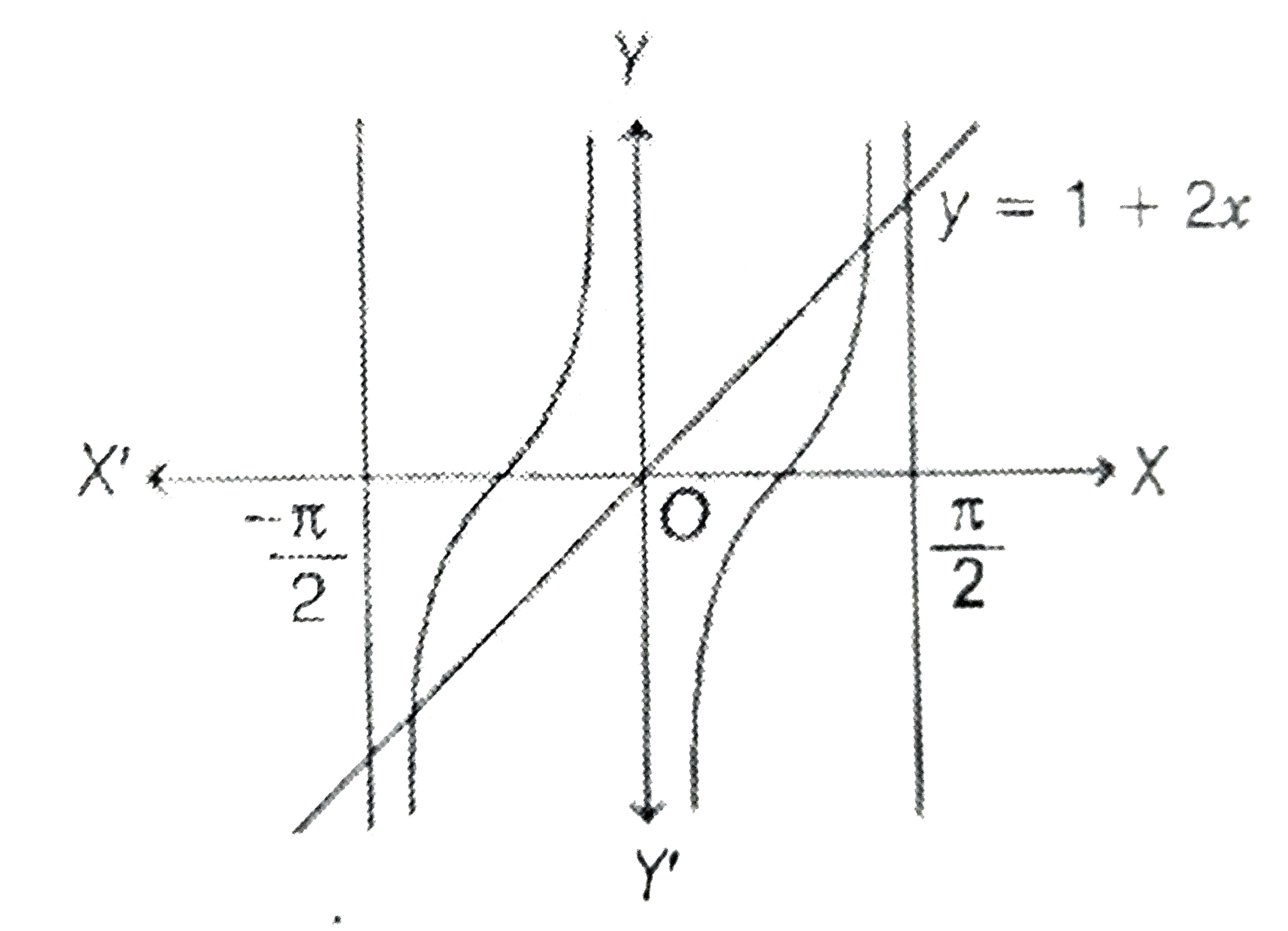
It is clear from the graph that y = tan x is one-one and onto, therefore (B)→(r).
Similar Questions
Let the function g:(−∞,∞)→(−π2,π2) be given by g(u)=2tan−1(eu)−π2. Then g is :
View SolutionFor relation 2logy−logx−log(y−1) a. Domain =[4,+∞),range-(1,+∞) b. Domain =[4,+∞), range- (2,+∞) c. Domain =(2,+∞) ,range-(2,+∞) d. None of these
View SolutionLet the province of the functions defined in column I (-pi//2,pi//2) And range (-oo,oo) is . Then match the conditions / expressions given in column I with the statements given in column II.
View SolutionLet the function defined in column 1 have domain (0,π/2) the

View SolutionLet the function g:(−∞,∞)→(−π2,π2) be given by g(u)=2tan−1(eu)−π2. Then g is :
View SolutionLet the function g,(−∞,∞)→(−π2,π2) be given by g(u)=2tan−1(eu)−π2, Then ,g is
View SolutionMatch List - I with List-II
Let the functions defined in List - I have domain (−π/2,π/2)

View SolutionIf function f(x) = (1+2x) has the domain (−π2,π2) and co-domain (−∞,∞) then function is
View Solution