A tangent to the ellipse x2 + 4y2 = 4 meets the ellipse x2 + 2y2 = 6 at P and Q. Prove that the tangents at P and Q of the ellipse x2 + 2y2 = 6 are at right angles.Solution in Tamil
given , x2+4y2=4orx24+y21=1
Equation of any tangent to the ellipse on(i) can be written as
x2cosθ+ysinθ=1
Equation of second ellipse is
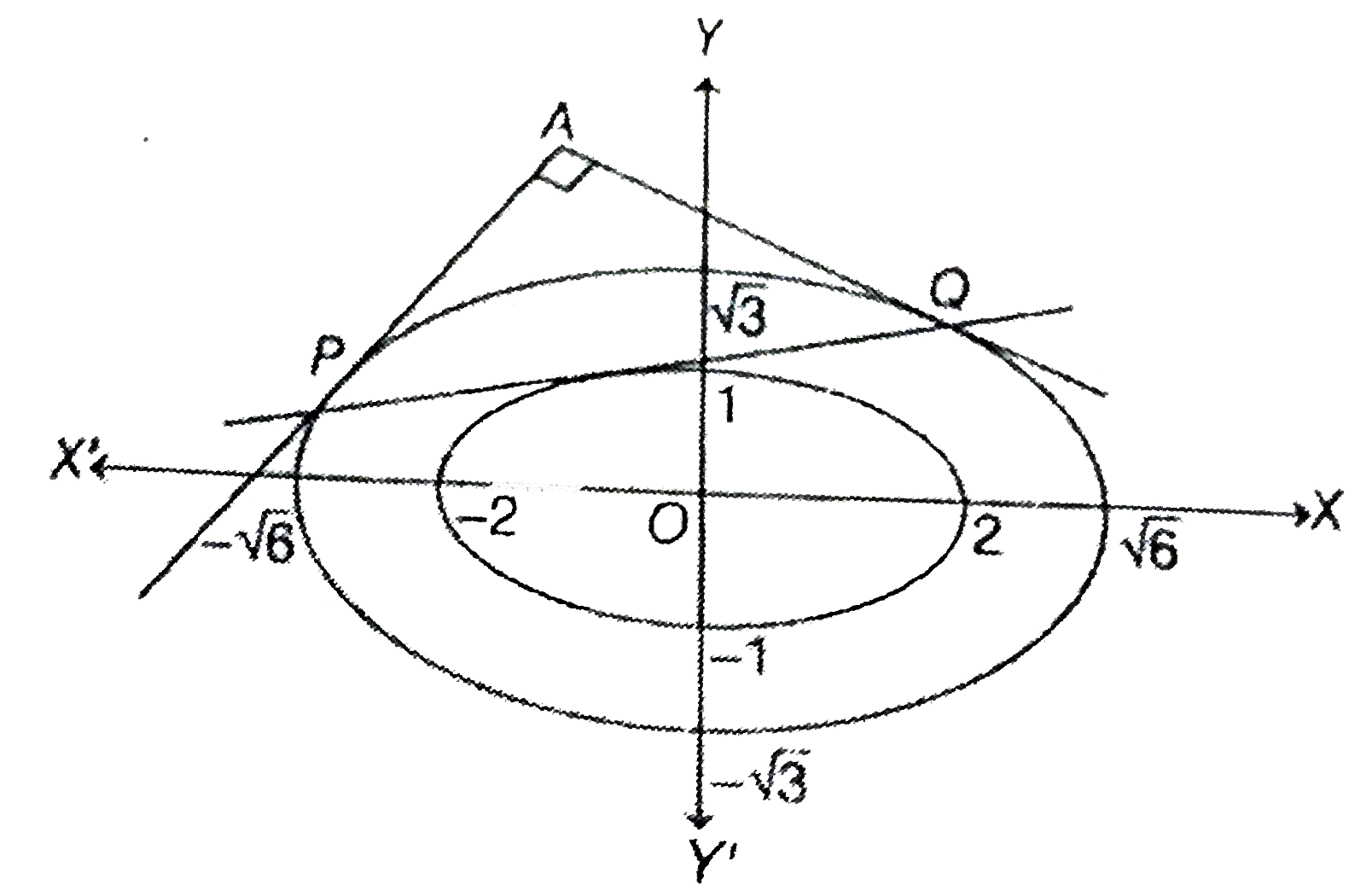
x2+2y2=6
⇒x26+y23=1
Suppose the tangent at P and Q meets at (h,k) Equation of the chord of contact of the tangents through A (h,k) is
hx6+ky3=1
But Eqs . (iv) and (ii) represent the same straight line , so comparing Eqs. (iv) adn (ii) we get
h/6cosθ/2=k/3sinθ=11
⇒h=3cosθandk=3sinθ
therefore , coordinates of A are ( 3 cos,θ,3sinθ)
Now , the joint equation of the tangents At A is given by T2=SS1,
i.e.,(hx6+ky3−1)2=(x26+y23−1)(h26+h23−1)
in Eq. (v) Coefficient of x2=h236−16(h26+h23−1))
=h236−h236−k218+16=16−k218
and coefficient of y2=k29−13(h26+k23−1)
=k29−h218−k29+13=−h218+13
Again , coefficient of x2+ coefficient of y2
=−118(h2+k2)+16+13
=−118(9cos2θ+9sin2θ+12
=−918+12=0
which shows that two lines represent by Eq. (v) are at right angles to each other .
Similar Questions
If any tangent to the ellipse makes intercepts of lengths p and q on the axes, prove that a2p2+b2q2=1
View SolutionA tangent to the ellipse x2+4y2=4 meets the ellipse x2+2y2=6 at P and Q. The angle between the tangents at P and Q of the ellipse x2+2y2=6 is
View SolutionA tangent to the ellipse x2+4y2=4 meets the ellipse x2+2y2=6 at P&Q.
View SolutionEllipse x^2 +4y^2 =4 One touch line ellipse x^2+2y^2= 6 Meets at P and Q. Prove that ellipse x^2+y^2 = 6 The tangent lines drawn at P and Q are at right angles.
View SolutionEllipse (x^(2))/(14)=(y^(2))/(5)=1 The tangent to the circle intersects the circle at two points P and Q. If the chord connecting P and B forms a right angle at the center, the ellipse of the ellipse will be
View Solutionदीर्घवृत्त x2+4y2=4 की स्पर्श रेखा, दीर्घवृत्त x2+2y2=6 को P तथा Q पर मिलती है। सिद्ध कीजिए कि P तथा Q पर दीर्घवृत्त x2+2y2=6 की स्पर्श रेखायें समकोण पर होंगी।
View Solutionदीर्घवृत्त x2+4y2=4 की स्पर्श रेखा, दीर्घवृत्त x2+2y2=6 को P व Q बिन्दुओं पर मिलती है। सिद्ध कीजिए कि P व Q पर दीर्घवृत्त x2+2y2=6 की स्पर्श रेखायें लम्बवत् होंगी।
View SolutionTwo parallel tangents of a circle meet a third tangent at points P and Q. Prove that PQ subtends a right angle at the centre.
View Solution
