Let F1(x1,0)andF2(x2,0) for x1<0andx2>0, be the foci of the ellipse x29+y28=1 . Suppose a parbola having vertex at the origin and focus at R2 intersects the ellipse at point lt in the first quadrant and point N in the fourth quadrant
The orthocentre of the triangle F1 MN is Solution in Tamil
(−910,0)
(23,0)
(910,0)
(23,√6)
The correct Answer is:A
Here , x29+y28=1
has foci (+ae,0)
where , a2e2=a2−b2
⇒a2e2=9−8
⇒ae=±1
i.e.,F1,F2=(±1,0)
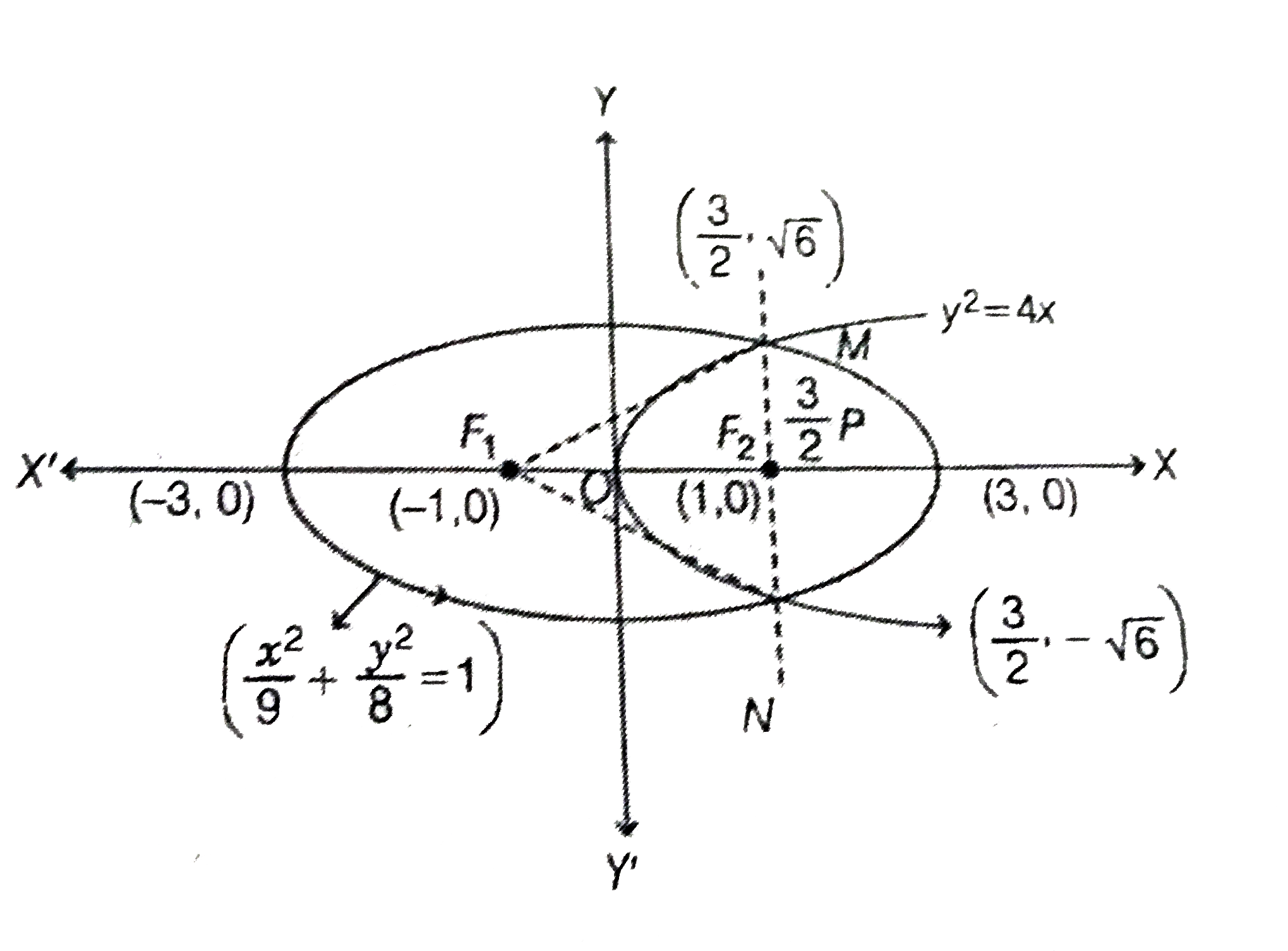
Equation of parabola having vertex O(0,0) and F2(1,0)(as,x2>0)
y2=4x
on solving x29+y28=1andy2=4x, we get
x=3/2andy=±√6
equation of altitude through M oin NF1 is
y−√6x−3/2=52√6
⇒(y−√6)=52√6(x−3/2). . .(iii)
and equilibrium of altitude through F1 is Y=0 . . .(iv)
on solving Eqs. (iii) and (iv) , we get (−910,0)as orthocentre.
Similar Questions
Let F1(x1,0) and F2(x2,0), for x1<0 and x2>0, be the foci of the ellipse x29+y28=1. Suppose a parabola having vertex at the orgin and focus at F2 intersects the ellipse at point M in the first quadrant and at point N in the fourth quadrant.
If the tangents to the ellipse at M and N meet at R and the normal to the parabola at M meets the x-axis at Q, then the ratio of area of the triangle MQR to area of the quadrilateral MF1NF2 is
View Solutionमाना कि F1(x1,0) और F2(x2,0), जिसमें x1<0,x2>0 दीर्घवृत्त (ellipse) x29+y28=1 की नाभियाँ (Foci) है | माना कि एक परवलय (parabola) जिसका शीर्ष (vertex) मूलबिन्दु (origin) पर और नाभि (focus) F2 पर है, दीर्घवृत को प्रथम चतुर्थाश (first quadrant) में M पर और चतुर्थ चतुर्थाश (fourth quadrant) में N पर प्रतिच्छेदित करता है |
त्रिभुज F1MN का लम्बकेन्द्र (orthocenter) है
View SolutionA , r = 1 , 2, 3 ….., n are n points on the parabola y^(2)=4x in the first quadrant . If A_(r) = (x_(r),y_(r)) where x_(1),x_(2),….x_(n) are in G.P and x_(1)=1,x_(2)=2 then y_(n) is equal to
View Solutionf1(x)=x+a,f2(x)=x2+bx+c and Δ=∣∣ ∣ ∣∣111f1(x1)f1(x2)f1(x3)f2(x1)f2(x2)f2(x3)∣∣ ∣ ∣∣, then Δ is independent of
View Solutionमाना कि F1(x1,0) और F2(x2,0), जिसमें x1<0,x2>0 दीर्घवृत्त (ellipse) x29+y28=1 की नाभियाँ (Foci) है | माना कि एक परवलय (parabola) जिसका शीर्ष (vertex) मूलबिन्दु (origin) पर और नाभि (focus) F2 पर है, दीर्घवृत को प्रथम चतुर्थाश (first quadrant) में M पर और चतुर्थ चतुर्थाश (fourth quadrant) में N पर प्रतिच्छेदित करता है |
त्रिभुज F1MN का लम्बकेन्द्र (orthocenter) है
View Solutionमाना कि F1(x1,0) और F2(x2,0), जिसमें x1<0,x2>0 दीर्घवृत्त (ellipse) x29+y28=1 की नाभियाँ (Foci) है | माना कि एक परवलय (parabola) जिसका शीर्ष (vertex) मूलबिन्दु (origin) पर और नाभि (focus) F2 पर है, दीर्घवृत को प्रथम चतुर्थाश (first quadrant) में M पर और चतुर्थ चतुर्थाश (fourth quadrant) में N पर प्रतिच्छेदित करता है |
त्रिभुज F1MN का लम्बकेन्द्र (orthocenter) है
View SolutionLet x1 and x2 are the roots of ax2+bx+c=0(a,b,cεR)andx1.x2<0,x1+x2 is non zero, then the roots of x1(x−x2)2+x2(x−x1)2=0 are
View SolutionF1andF2 are the two foci of the ellipse x29+y24=1. Let P be a point on the ellipse such that |PF1|=2|PF2|, where F1andF2 are the two foci of the ellipse . The area of △PF1F2 is :
View Solution