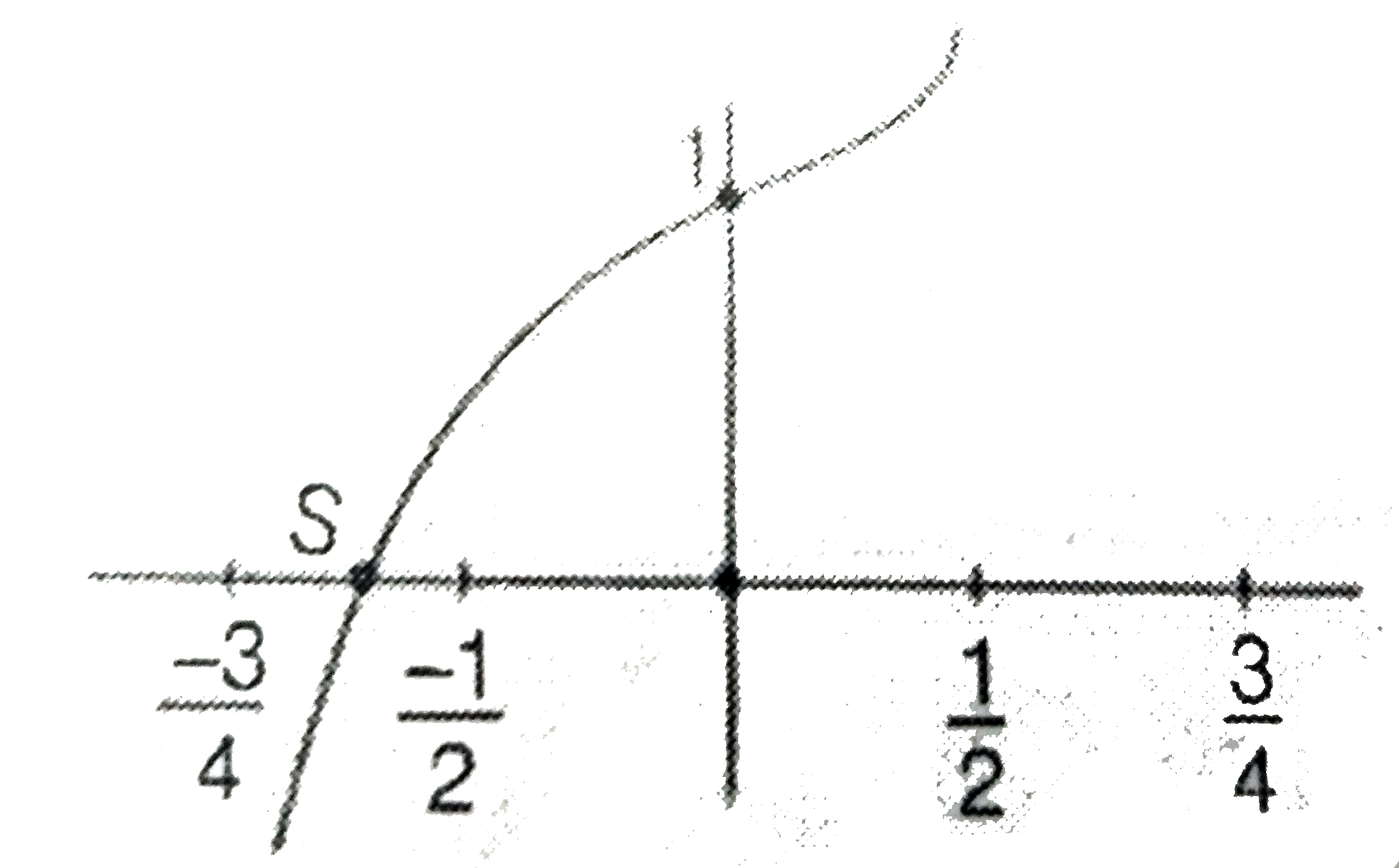
Consider the polynomial f(x)=1+2x+3x2+4x3. Let s be the sum of all distinct real roots of f(x)and let t=|s|.Solution in Tamil
increasing in (−t,−14) and decreasin in (−14,t)
decreasing in (−t,−14) and decreasing in (−14,t)
increasing in (−t,t)
decreasing in (−t,t)
The correct Answer is:B
As, f''(x)=2(12x+3)
f'(x)>0,whenx>−14andf'(x)<0,whenx<−14.
∴ It could be shown as
Similar Questions
दिया है बहुपद f(x)=1+2x+3x2+4x3.
माना कि f(x) के भिन्न, वास्तविक मूलो का योग S है तथा t=|S| है |
Q. वास्तविक संख्या S, निम्न अन्तराल में है
View Solutionदिया है बहुपद f(x)=1+2x+3x2+4x3.
माना कि f(x) के भिन्न, वास्तविक मूलो का योग S है तथा t=|S| है |
Q. वक्र y=f(x) तथा सरल रेखाओ x=0, y=0 एवं x=t से सीमित क्षेत्र का क्षेत्रफल निम्न अंतराल में है
View Solutionदिया है बहुपद f(x)=1+2x+3x2+4x3.
माना कि f(x) के भिन्न, वास्तविक मूलो का योग S है तथा t=|S| है |
Q. फलन f'(x)
View SolutionConsider the polynomial f(x)=1+2x+3x2+4x3. Let s be the sum of all distinct real roots of f(x)and let t=|s|.
View SolutionConsider the polynomial f(x)=1+2x+3x2+4x3. Let s be the sum of all distinct real roots of f(x)and let t=|s|.
View SolutionConsider the polynomial f(x)=1+2x+3x2+4x3 for all x∈R So f(x) has exactly one real root in the interval
View SolutionConsider the polynomial f (x)= 1+2x+3x^2+4x^3 . Let s be the sum of all distinct real roots of f(x) and let t= |s| . The real number s lies in the interval. (a) (- 1/4, 0) (b) (- 11, - 3/4) (c) (- 3/4, - 1/2) (d) (0, 1/4)
View SolutionConsider the polynomial f (x)= 1+2x+3x^2+4x^3 . Let s be the sum of all distinct real roots of f(x) and let t= |s| .
View Solution
