Let S be the set of all non-zero numbers αsuch that the quadratic equation αx2−x+α=0has two distinct real roots x1,andx2 satisfying the inequality |x1−x2|<1 which of the following intervals is(are) a subset of S?Solution in Tamil
(−12,−1√5)
(−1√5,0)
(0,1√5)
(1√5,12)
The correct Answer is:A, D
Given,x1andx2 are roots of ax2−x+α=0.
∴x1+x2=1αandx1x2=1
Aslo,|x1−x2|<1
⇒|x1−x2|2<1⇒(x1−x2)2<1
or(x1+x2)2−4x1x2<1
⇒1α2−4<1or1α2<5
⇒5α2−1>0or(√5α−1)(√5α+1)>0
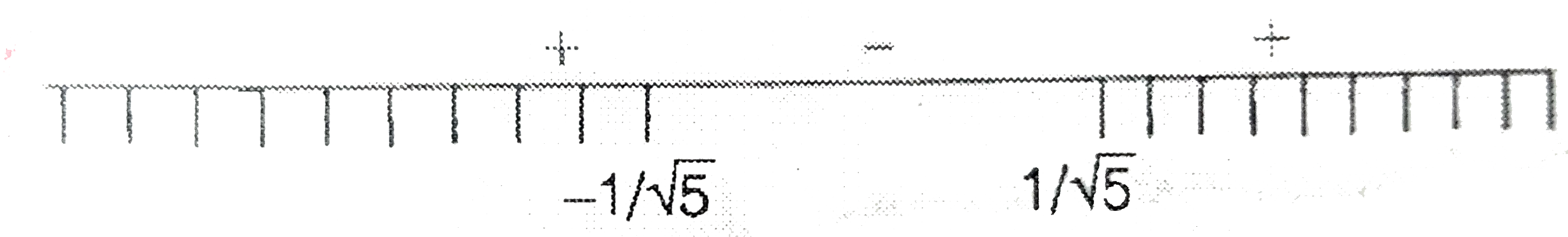
∴α∈(−∞o,−1√5)∪(1√5,∞) ...(i)
Also, ⇒1−4α2>0orα∈(−12,12) ...(ii)
From Eqs. (i) and ?(ii), we get
α∈(−12,−1√5)∪(1√5,12)
Similar Questions
If b<0, then the roots x1 and x2 of the equation 2x2+6x+b=0, satisfy the condition (x1x2)+(x2x1)<k where k is equal to
View SolutionLet S be the set of all non-zero real numbers α such that the quadratic equation αx2−x+α=0 has two distinct real roots x1 and x2 satisfying the inequality |x1−x2|<1. Which of the following intervals is (are) a subset(s) of S ?
View SolutionIf x1andx2 are the real and distinct roots of ax2+bx+c=0, then prove that limn→x1{1+sin(ax2+bx+c)}1x−x1=ea(x1−x2)
View SolutionLet S be the set of all non-zero real numbers such that the quadratic equation αx2−x+α=0 has two distinct real roots x1andx2 satisfying the inequality |x1−x2|<1. Which of the following intervals is (are) a subset (s) of S? (12,1√5) b. (1√5,0) c. (0,1√5) d. (1√5,12)
View SolutionFind a quadratic equation whose product of roots x1 and x2 is equal to 4 an satisfying the relation x1x1−1+x2x2−1=2.
View SolutionLet S be the set of all non-zero numbers αsuch that the quadratic equation αx2−x+α=0has two distinct real roots x1,andx2 satisfying the inequality |x1−x2|<1 which of the following intervals is(are) a subset of S?
View SolutionFind a quadratic equation whose product of roots x1andx2 is equal to 4 and satisfying the relation x1x1−1+x2x2−1=2.
View Solution
