A swimmer S is in the sea at a distance dkm from the closest point A on a straight shore. The house of the swimmer is on the shore at distance Lkm from A. He can swim at speed of ukm/h. walk at speed at vkm/h. At what point on shore should he land so that hhe reaches his house in the shortest time. Solution in Tamil
The correct Answer is:L−ud√v2−u2 km from his house
Let the swimmer lands at the point P,x km from A and when walks from P to the point B to be reached

Given that AB=L km.Thenn PB =(L-x)km
T=Total time from S to B
=(Time taken from S to P) +(Time taken from P to B) =SPu+PBv
∴dtdx=xu√d2+x2−1v
for maximum or minimum of t,d/dx=0
or x=ud√v2−u2
Therefore t is minimum for this for the value of x (sinced2tdx2is+ve)
time if he lands at distane L−x=L−udv2−u2 form his house to be reached
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise 6.7
5 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Single)
93 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise 6.5
5 Videos
- METHODS OF DIFFERETIATIONBOOK - CENGAGECHAPTER - METHODS OF DIFFERETIATIONEXERCISE - Question Bank
13 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
A metal box with a square base and vertical sides is to contain 1024 cm3 of water, the material for the top and bottom costs Rs 5 per cm2 and the material for the sides costs Rs 2.50 per cm2. Find the least cost of the box.
View SolutionA function is matched below against an interval where it is supposed to be increasing. Which of the following parts is incorrectly matched? Interval, Function (a)[2, ∞) , 2x3−3x2−12x+6 (b)(−∞,∞) , x3=3x2+3x+3 (c)(−∞−4) , x3+6x2+6 (d)(−∞,13) , 3x2−2x+1
View SolutionDraw the graph of f(x)=(x−1)|(x−2)(x−3)|. .
View SolutionLet f:(−5,5)→R be a differentiable function with f(4) = 1, f′(4)=1,f(0)=−1 and f^(')(0) = 1,Ifg(x) = f(2f^(2)(x)+2))^(2),then - g^(')(0) equals
View SolutionLet f:R→R,y=f(x),f(0)=0,f'(x)>0andf''(x)>0. Three point A(α,f(α)),B(β,f(β)),C(γ,f(γ))ony=f(x) such that 0<α<β<γ.
Which of the following is false ?
View SolutionA swimmer S is in the sea at a distance dkm from the closest point A on a straight shore. The house of the swimmer is on the shore at distance Lkm from A. He can swin at speed oh ukm/h. walk at speed at vkm/h. At what point on shore should he land so that hhe reaches his house in the shortest time.
View SolutionA swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. The man has to reach the other shore at the point directly opposite to his starting point. If the reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
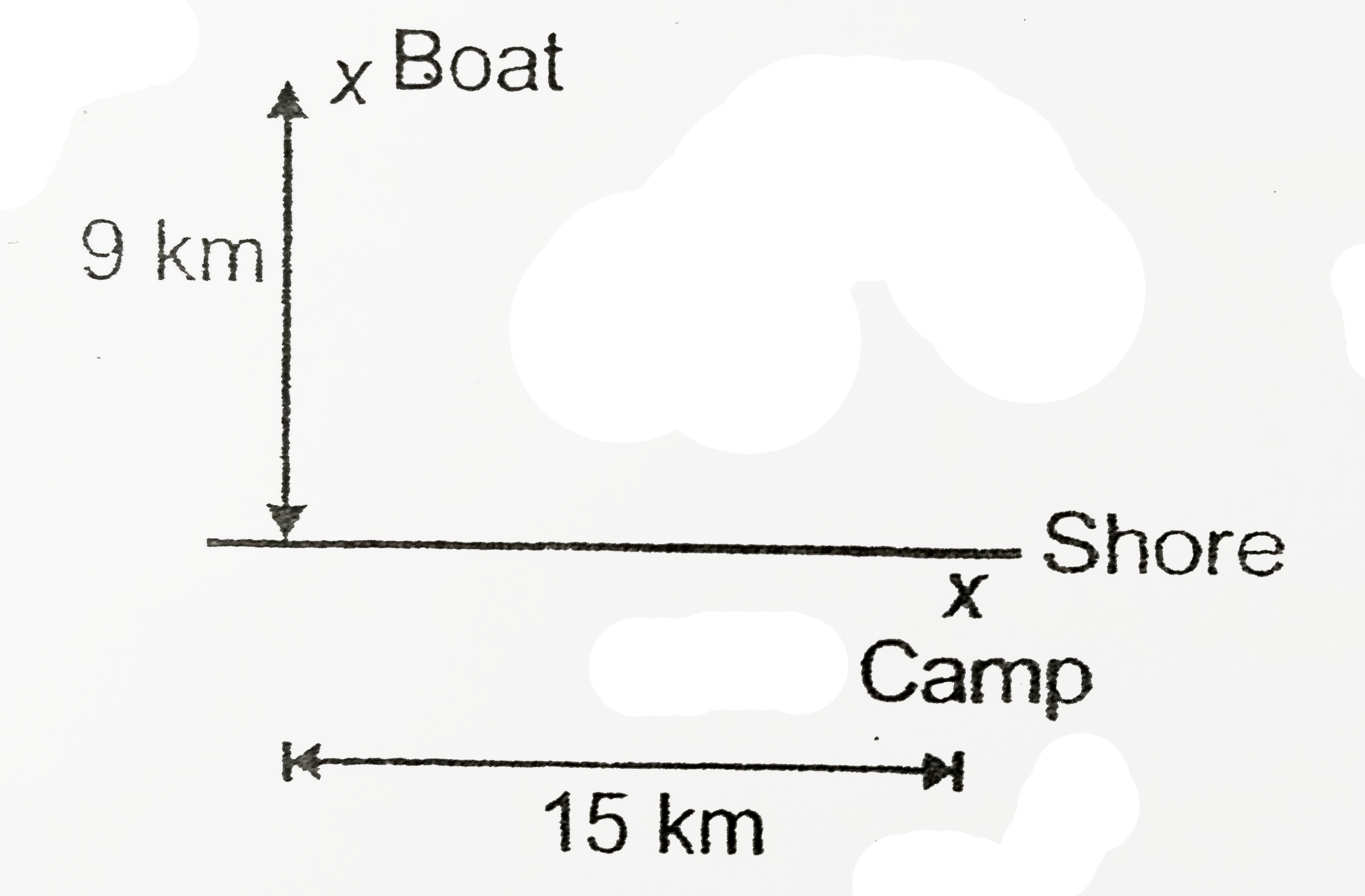
View SolutionA fishing boat is anchored 9 km away from the the nearest point on the shore. A messanger must be sent from the fishing boat to a camp, 15 km from the point on shore closest to boat. If the messanger can walk at a speed of 5 km per hour and can row at 4 km/h. determine the distance of that point (in km) from the shore, where he must land so as to reach the shore in least possible time.
View Solutionएक तैराक 5 km/h वेग से बह रही 500 m चौड़ी नदी को तैरकर पार करना चाहता है ।
तैराक को पैदल या तैरकर प्रारंभिक बिंदु के ठीक सामने दूसरे किनारे पर पहुँचना है । यदि वह तैरकर इस बिंदु से दूर कही निकलता है , तो उसे पैदल चलकर इस बिंदु तक आना पड़ेगा । उसे कम-से-कम कितनी दुरी पैदल चलना पड़ेगा ?
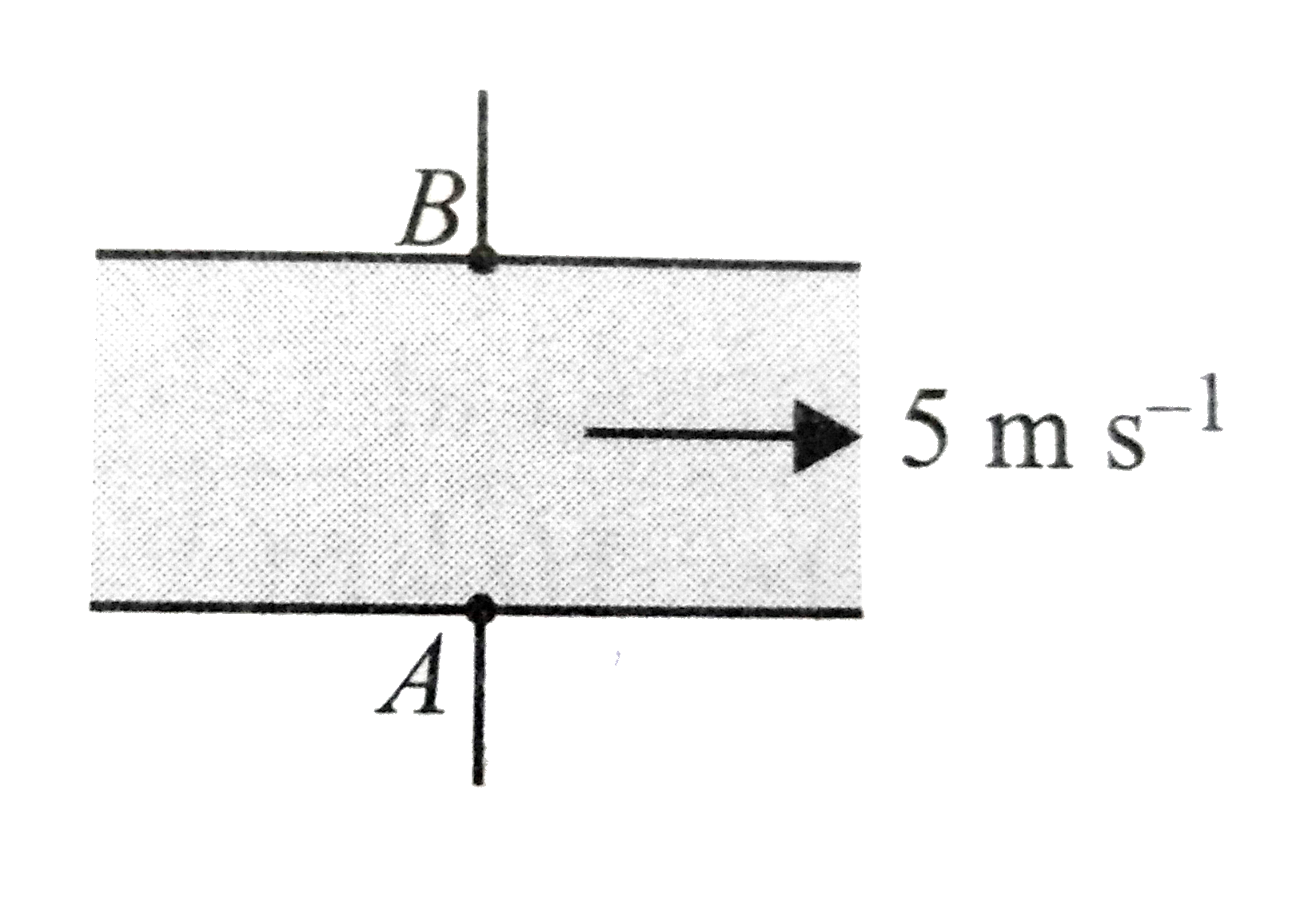
View SolutionA river is flowing from west to east with a speed 5 m s−1. A swimmer can swim in still water at a speed of 10 m s−1 .
If he wants to start from point A on south bank and reach opposite point B on north bank. In what direction direction should he swim ?
View SolutionA man of mass 60 kg is standing on a boat of mass 140 kg, which is at rest in still water. The man is initially at 20 m from the shore. He starts walking on the boat for 4 s with constant speed 1.5 m/s towards the shore. The final distance of the man from the shore is
View Solutionएक तैराक S समुद्र में सीधे किनारे पर निकटतम बिन्दु A से d km दूरी पर है। तैराक का घर किनारे पर A से L km दूरी । पर है। वह ukm/hr की गति से तैर सकता है तथा vkm/hr(v>u) की गति से चल सकता है। वह किनारे पर किस बिन्दु पर उतरे ताकि वह अपने घर पर सबसे कम संभव समय में पहुँच जाए ?
View SolutionA swimmer S is in the sea at a distance d km from the closest point A on a straight shore The house of the swimmer is at a distance Lkm from A on the shore. He can swim at a speed of ukm/hr and walk at a speed of vkm/hr(v>u). At what point on the shore should he land so that he reaches his house in the shortest possible time?
View SolutionA woodrn log of mass 120 kg is floating on still water perpendicular to the shore. A man of mass 80 kg is standing at the centre of mass of the log and he is at a distance of 30 m from the shore. When he walks through a distance of 10 m towards the shore and halts, now his distance from the shore is
View SolutionA wooden log of mass 120kg is floating on still water perpendicular to the shore. A man of mass 80kg is standing at the centre of mass of the log and he is at a distance of 30m from the shore. When he walks through a distance of 10m towards the shore and halts, now his distance from the shore is
View SolutionA wooden log of mass 120kg is floating on still water perpendicular to the shore. A man of mass 80kg is standing at the centre of mass of the log and he is at a distance of 30m from the shore. When he walks through a distance of 10m towards the shore and halts, now his distance from the shore is
View Solution
