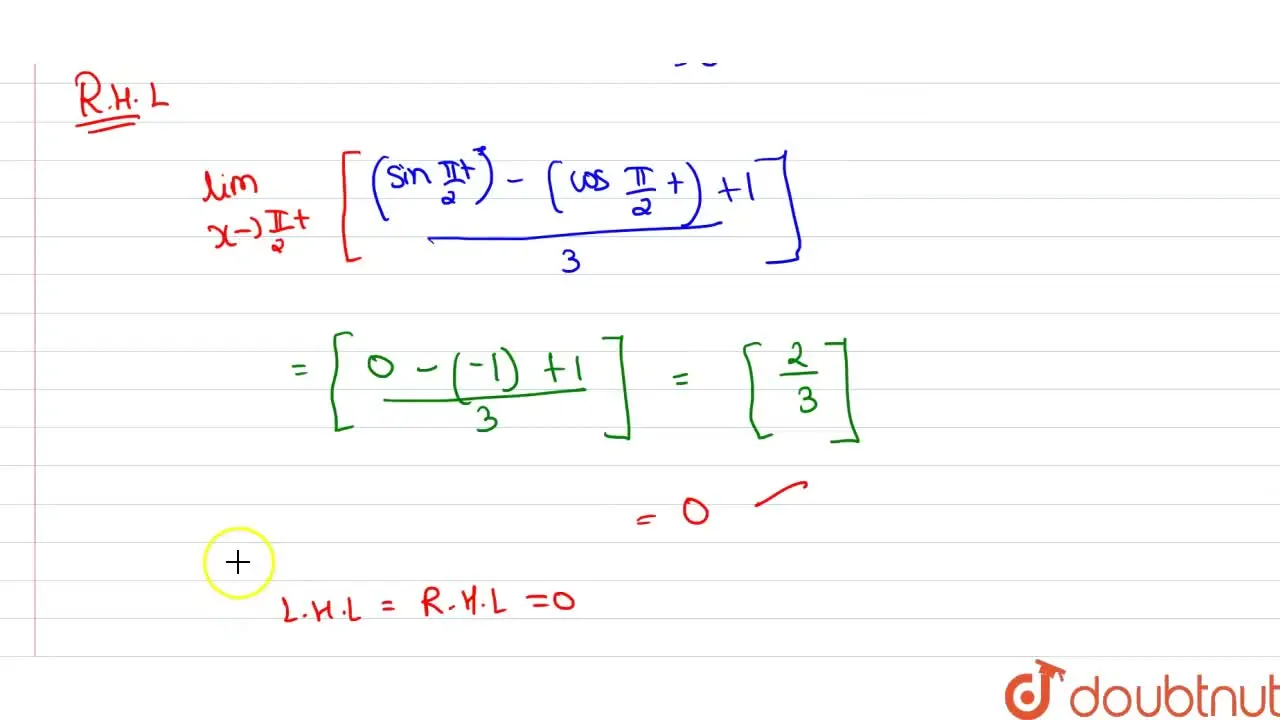limx−π2[[sinx]−[cosx]+13]= (where [.] denotes the greatest integer integer function)Solution in Tamil
0
1
−1
does not exist
The correct Answer is:A
limx→π+2[[sinx]−[cosx]+13]=[0−(−1)+13]=0
limx→π−2[[sinx]−[cosx]+13]=[0−0+13]=0
∴ limx→π2[[sinx]−[cosx]+13]=0
Related Playlists
- BOOK - CENGAGECHAPTER - LIMITSEXERCISE - Multiple Correct Answers Type4videos
LIMITS
- BOOK - CENGAGECHAPTER - LIMITSEXERCISE - ComprehensionType2videos
LIMITS
- BOOK - CENGAGECHAPTER - LIMITSEXERCISE - JEE Advanced Previous Year7videos
LIMITS
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
- BOOK - CENGAGECHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.210videos
LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORS
Similar Questions
If A=limx→0sin−1(sinx)cos−1(cosx)andB=limx→0[|x|]x, then
02:35View SolutionLet f(x) be the fourth degree polynomial such that f'(0)=−6,f(0)=2andlimx→1f(x)(x−1)2=1
The value of f(2) is01:06View SolutionIf limx→0[1+xln(1+b2)]1/x=2bsin2θ,b>0, and θ∈(−π,π], then the value of θ is
04:06View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
02:27View SolutionThe number of integral values of p for which (p+1)ˆi−3ˆj+pˆk,pˆi+(p+1)ˆj−3ˆk and −3ˆi+pˆj+(p+1)ˆk are linearly dependent vectors is q
04:15View SolutionThe function f(x)=1+x(sinx)[cosx],0<x≤π/2, where [.] denotes greatest integer function
04:19View Solutionlimx→π/2[x2]loge(sinx) (where [.] denotes the greatest integer function)
02:08View Solutionlimx−π2[[sinx]−[cosx]+13]= (where [.] denotes the greatest integer integer function)
06:04View Solutionlimx→0sin[cosx]1+[cosx], ([.] denotes the greatest integer function)
View SolutionThe value of limx→π2[x3]ln(sinx) (where, [.] denotes the greatest integer function)
02:02View SolutionThe value of limx→π2[x3]ln(1+cotx) is equal to (where, [.] denotes the greatest integer function )
01:51View Solutionlimx−π2[[sinx]−[cosx]+13]= (where [.] denotes the greatest integer integer function)
11:23View SolutionIf f(x)=(x(sinx+tanx))/([(x+pi)/(pi)]1/2) Where [] denotes the greatest integer function
02:24View SolutionThe number of solutions of [sinx+cosx]=3+[−sinx]+[−cosx] (where [.] denotes the greatest integer function ) x∈[0,2π]is
02:42View SolutionSolve
limx→0+[sinxx]
(where [.] denotes greatest integer function.)02:04View SolutionSolve
limx→0−[sinxx]
(where [.] denotes greatest integer function.)02:22View Solution