Question

A point moves such that the sum of the square of its distances from two fixed straight lines intersecting at angle $2\alpha$ is a constant. Prove that the locus of points is an ellipse

Explanation

Let us chosse the point of intersection of the givne lines as the origin and their angular bisector as the x-axis. Thenequation of the two lines will bey mx and y=-mx , where = `tan alpha`,

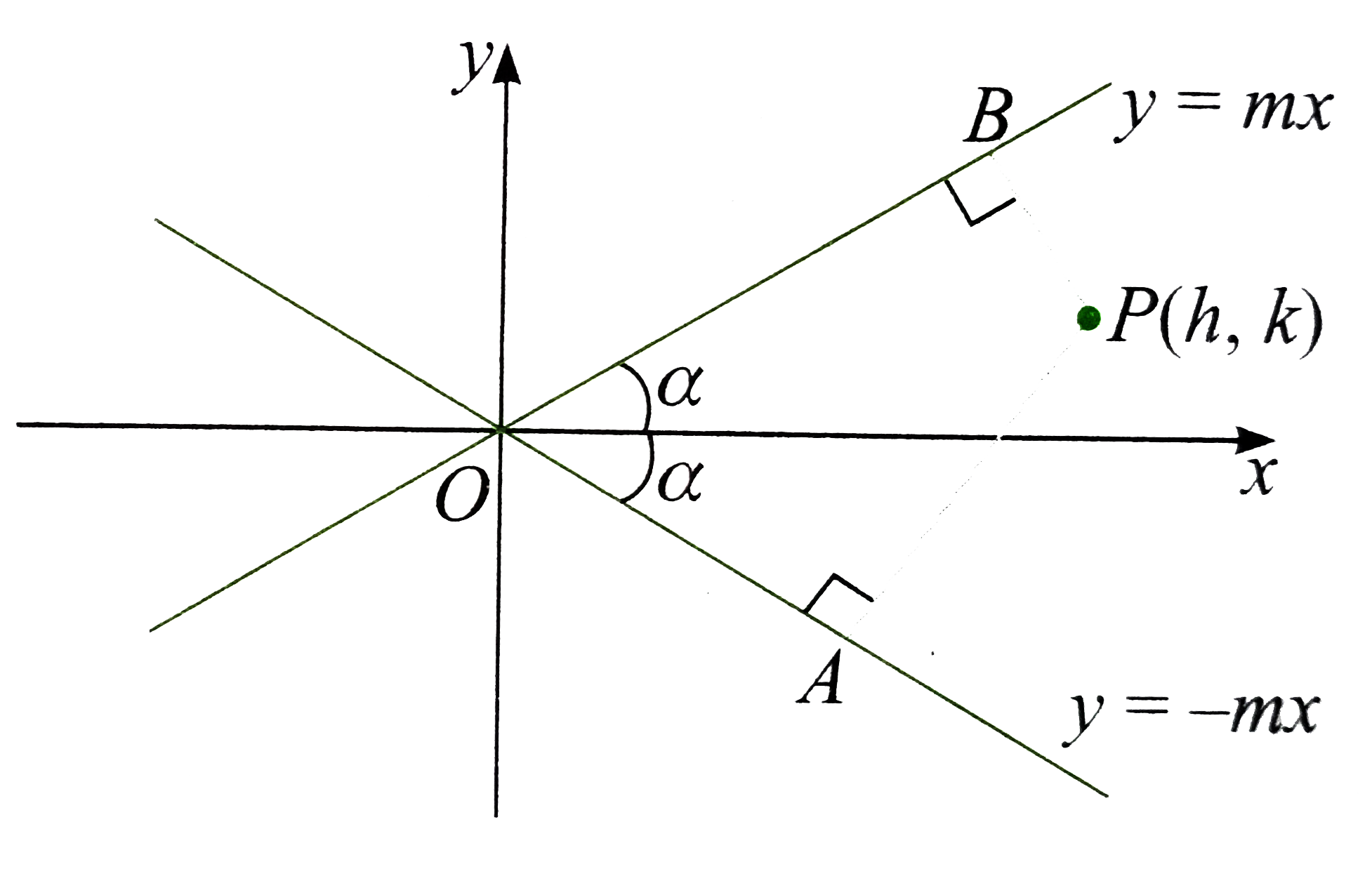
Let P(h,k) be the point whose locus is to be foud.
Then accroding toe the given condition,
`PA^(2)+PB^(2)`= Constant
`rArr((k-mh)^(2))/(1+m^(2))+((k+mh)^(2))/(1+m^(2))" " ("c is constant")`
`rArr 2(k^(2)+m^(2)h^(2))=c(1+m^(2))`
Therfore, the locus of pointP is
`(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`
where `a^(2)=(c(1+m^(2)))/(2m^(2)) and b^(2)=(c(1+m^(2)))/(2)` M
If `alpha lt pi //4`, then `m lt1, and a^(2)gtb^(2)`
`:.` Ecentricity `=sqrt(1-(b^(2))/(a^(2)))=sqrt(1-m^(2))=(sqrt(cos2alpha))/(cos alpha)`
If `alpha gt pi//4` then `mgt1 and a^(2)ltb^(2)`
`:.` Ecentricity `=sqrt(1-(b^(2))/(a^(2)))=sqrt(1-(1)/(m^(2)))=(sqrt(-cos 2 alpha))/(sin alpha)`