The two circles x2+y2=axandx2+y2=c2(c>0) touch each other if (1) a=2c (2) |a|=2c (3) 2|a|=c (4) |a|=c Solution in Tamil
|a|=2c
2|a|=c
|a|=c
a=2c
The correct Answer is:3
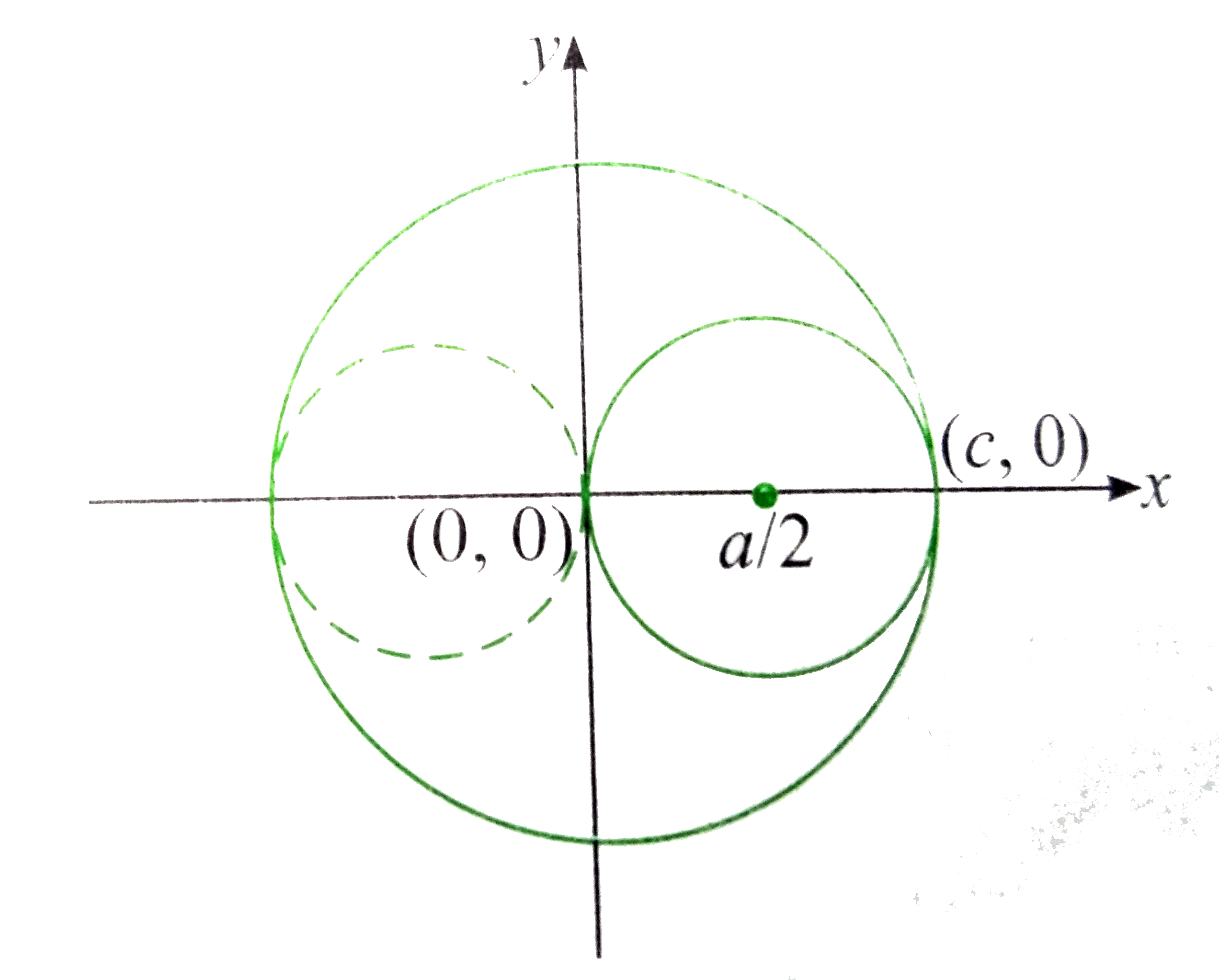
The figure is self-explanatory, Clearly c=|a|
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
6 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Numerical)
18 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
Tangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A&B ifR is the radius of circum circle of triangle PAB then [R]-
View SolutionFind the derivative of y=ln(cosx2).
View SolutionLet the lines (y−2)=m1(x−5) and (y+4)=m2(x−3) intersect at right angles at P (where m1andm2 are parameters). If the locus of P is x2+y2gx+fy+7=0 , then the value of |f+g| is__________
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionThe two circles x2+y2=ax and x2+y2=c2(c>0) touch each other if : (1) 2|a|=c (2) |a|=c (3) a=2c (4) |a|=2c
View SolutionIf the circles x2+y2+2ax+c=0andx2+y2+aby+c=0 touch each other then show that 1a2,12c,1b2 are in A.P.
View SolutionIf two circles x2+y2−2ax+c==0 and
x2+y2−2by+c=0 touch each other , then c =
View SolutionThe two circles x2+y2=ax,x2+y2=c2(c>0) touch each other if
View SolutionThe two circles : x2+y2=ax and x2+y2=c2 (c > 0) touch each other if :
View SolutionThe equation of the circle which touches the axes of coordinates and the line x3+y4=1 and whose center lies in the first quadrant is x2+y2−2cx−2cy+c2=0 , where c is (a) 1 (b) 2 (c) 3 (d) 6
View SolutionThe equation of the circle which touches the axes of coordinates and the line x3+y4=1 and whose center lies in the first quadrant is x2+y2−2cx−2cy+c2=0 , where c is (a) 1 (b) 2 (c) 3 (d) 6
View SolutionThe two circles x2+y2=axandx2+y2=c2(c>0) touch each other if (1) a=2c (2) |a|=2c (3) 2|a|=c (4) |a|=c
View SolutionThe equation of the circle which touches the axes of coordinates and the line x3+y4+=1 and whose centres lie in the first quadrant is x2+y2−2cx−2cy+c2=0, where c is equal to 4 (b) 2 (c) 3 (d) 6
View SolutionProve that the circles given by x2+y2+2ax+2by+c=0, and x2+y2+2bx+2ay+c=0, touch each other, if (a + b)^2 = 2c.
View Solution
