Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is Solution in Tamil
x2+y2=a2
x2+y2=2a2
x2+y2=4a2
x2+y2=8a2
The correct Answer is:3

The locus of the point of intersection of tangents at A and C is a circle whose center is O(0,0) and radius is
OT=acosec.π6=2a
So, the locus is x2+y2=4a2.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)
1 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Numerical)
18 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
Let C1 and C2 be two circles whose equations are x2+y2−2x=0 and x2+y2+2x=0 and P(λ,λ) is a variable point
View SolutionLet the lines (y−2)=m1(x−5) and (y+4)=m2(x−3) intersect at right angles at P (where m1andm2 are parameters). If the locus of P is x2+y2gx+fy+7=0 , then the value of |f+g| is__________
View Solutionabout to only mathematics
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionTangents PA and PB are drawn to a circle with point P outside the circle,line joining P and centre intersect chord AB at M then,Prove that /_OPA=/_OAM
View SolutionTwo variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
View SolutionAB is a chord of the circle x^(2)+y^(2)=9 .The tangents at A and B intersect at C. If M(1,2) is the midpoint of AB,then the area of triangle ABC is
View Solutionएक वृत्त, एक चतुर्भुज ABCD की चारों भुजाओं को अन्तः स्पर्श करता है। सिद्ध कीजिए कि-
AB + CD = AD + BC.
(अथवा) आकृति, में एक चतुर्भुज ABCD, O केन्द्र वाले वृत्त के परिगत इस प्रकार बनाई गई है कि भुजाएँ AB, BC, CD, तथा DA वृत्त को क्रमशः बिन्दुओं P, Q, R तथा S पर स्पर्श करती हैं। सिद्ध कीजिए कि
AB + CD = BC + DA

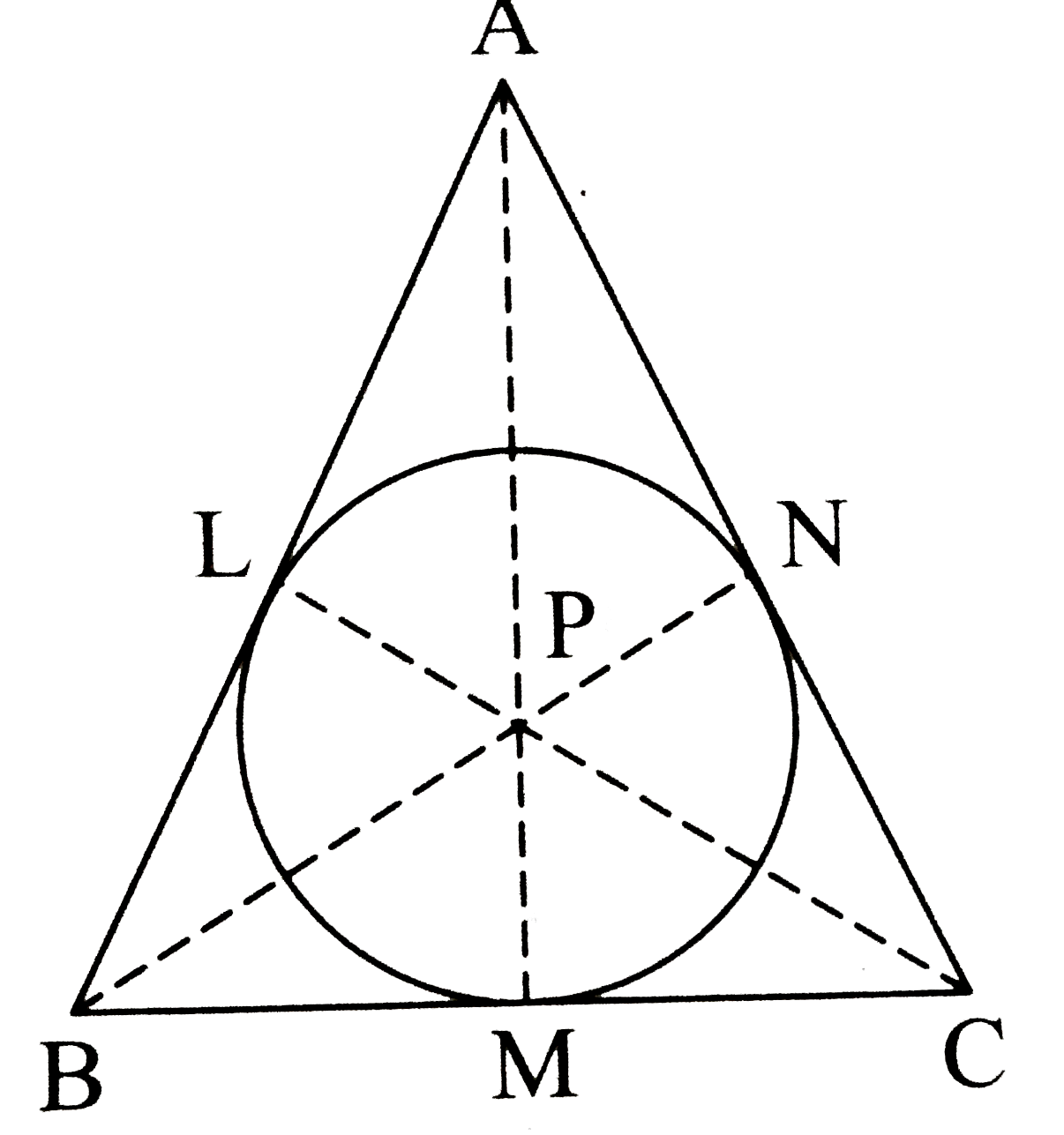
View SolutionA circle with centre P is inscribed in the ΔABC Side AB, side BC and side A C touch the circle at points L,M and N respectively . Prove that :
A(ΔABC)=12(AB+BC+AC)×r
View SolutionAB is a diameter of a circle. BP is a tangent to the circle at B. A straight line passing through A intersects BP at C and the circle at D. Prove that BC2=AC×CD.
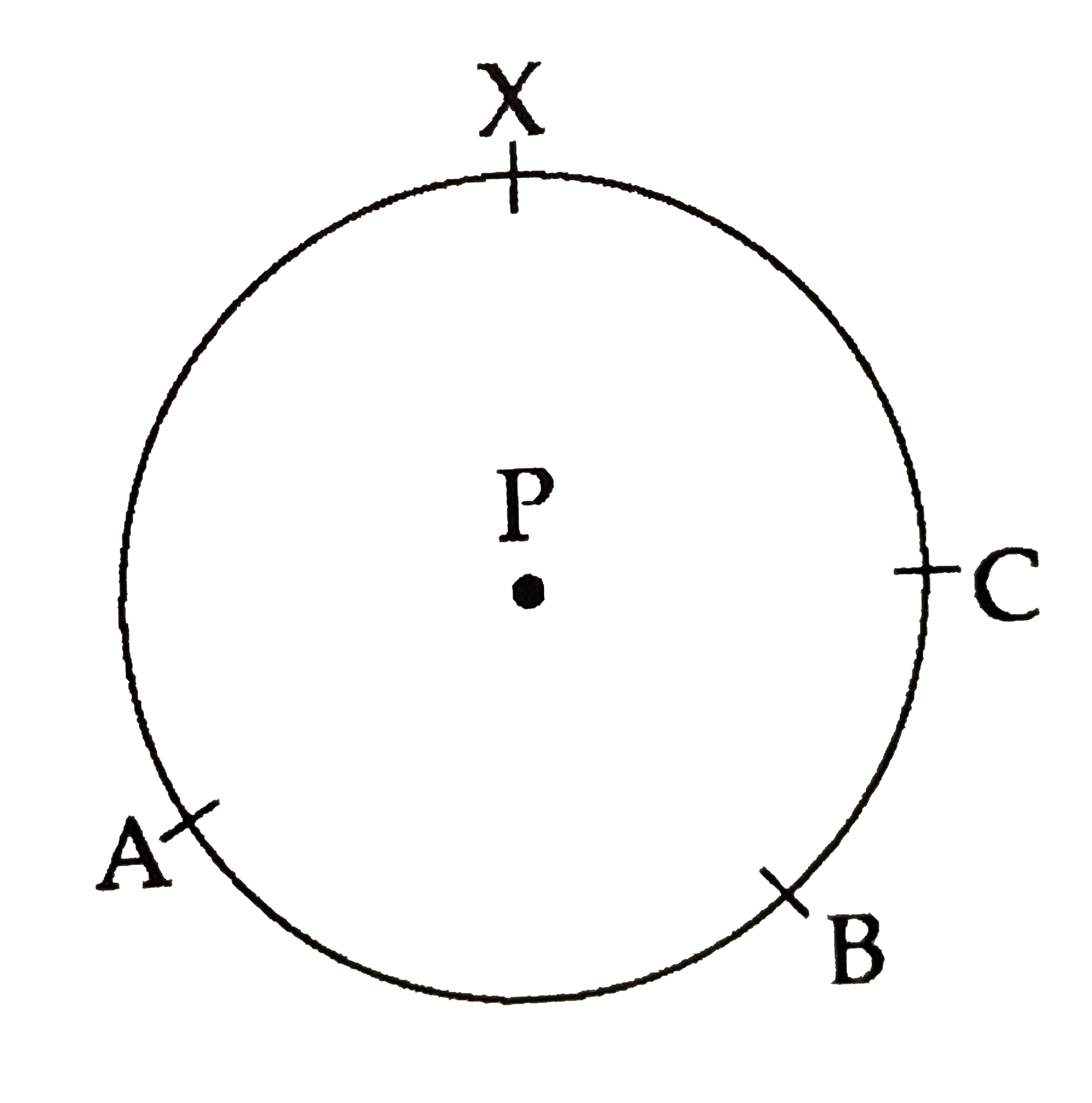
View SolutionA circle with centre P. arc AB = arc BC and arc AXC = 2 arc AB . Find measure of arc AB, arc BC and arc AXC. Prove that chord AB≅ chord BC .
View Solutionदो सकेंद्रिय व्रतों में बड़े वृत की जीवा AB, बिंदु P पर छोटे की सपरशरेखा है | दिखायें P, AB का मध्यबिंदु है |
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a ,then locus of point of intersection of tangents at A and C is a circle of radius λa, where λ is
View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
View Solution
