A line meets the coordinate axes at $A$ and $B$ . A circle is circumscribed about the triangle $O A B .$ If $d_{1} a n d d_{2}$ are distances of the tangents to the circle at the origin $O$ from the points $A a n d B$ , respectively, then the diameter of the circle is $\frac{2 d_{1} + d_{2}}{2}$ (b) $\frac{d_{1} + 2 d_{2}}{2}$ $d_{1} + d_{2}$ (d) $\frac{d_{1} d_{2}}{d_{1} + d_{2}}$ Solution in Tamil

A

$\frac{2 d_{1} + d_{2}}{2}$

B

$\frac{d_{1} + 2 d_{2}}{2}$

C

$d_{1} + d_{2}$

D

$\frac{d_{1} d_{2}}{d_{1} + d_{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:3

Let the circle be $x^{2} + y^{2} + 2 g x + 2 f y = 0$ .

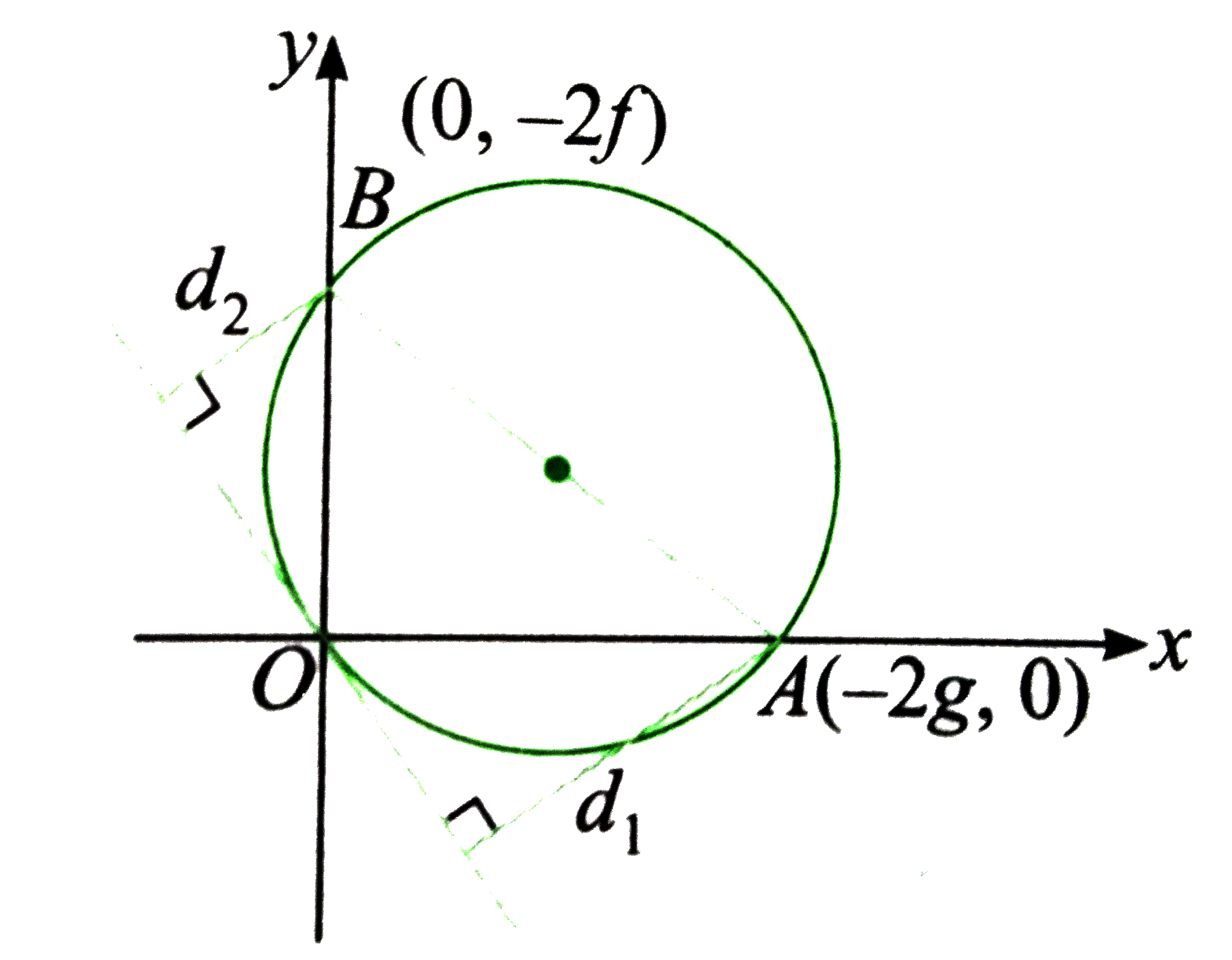
Tangent at the origin is
$g x + f y = 0$
$d_{1} = \frac{2 g^{2}}{\sqrt{g^{2} + f^{2}}}$ and $d_{2} = \frac{2 f^{2}}{\sqrt{g^{2} + f^{2}}}$
or $d_{1} + d_{2} = 2 \sqrt{g^{2} + f^{2}}$
$=$ Diameter of the circle

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

CENGAGE-CIRCLE -Exercise (Single)

Home
Ask Doubt
Profile