If is the origin and are the tangents from the origin to the circle , then the circumcenter of triangle is (b) (d) Solution in Tamil
The correct Answer is:2
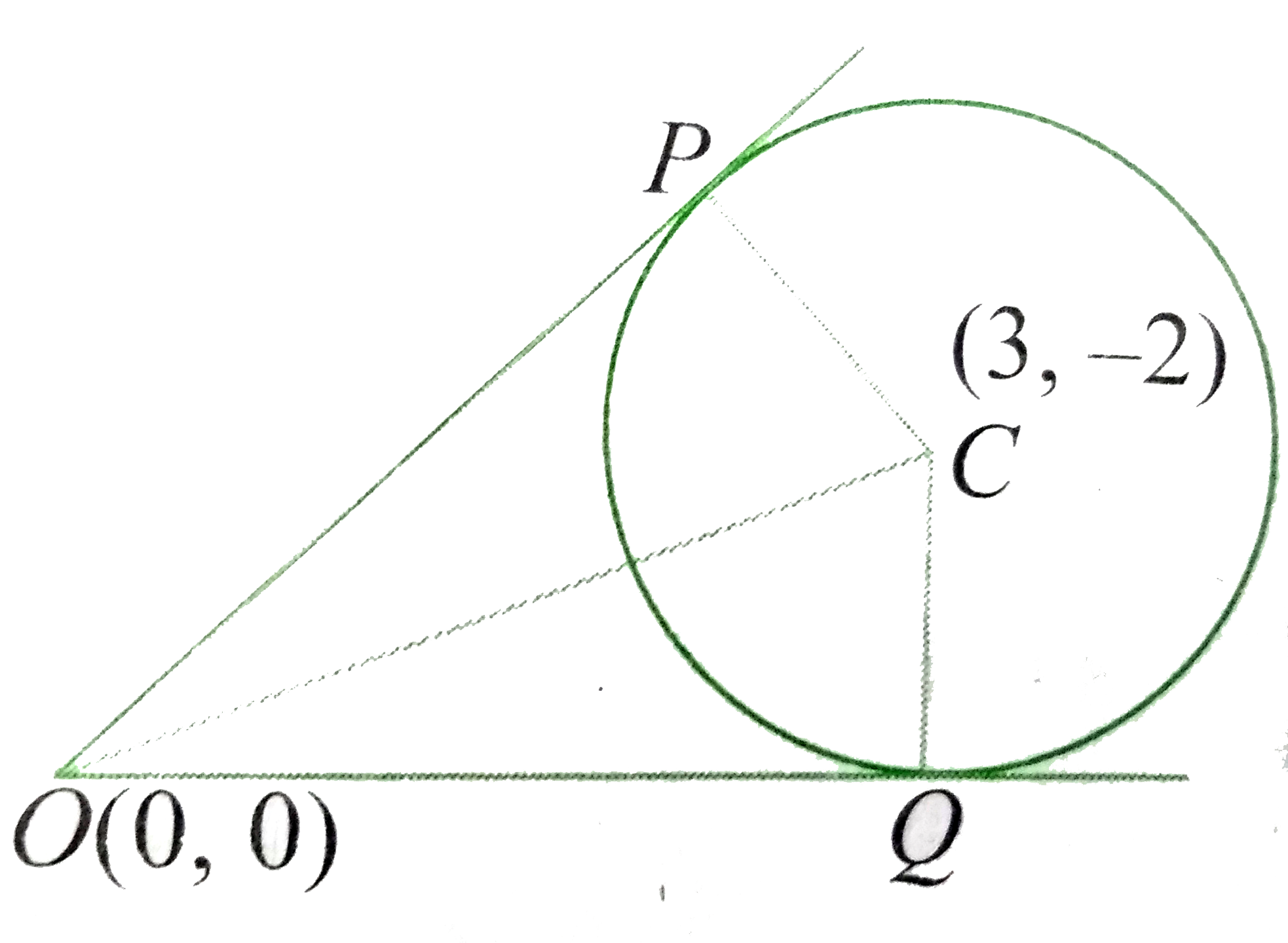
Clearly, OPCQ is a cyclic quadrilateral. Then the circumcircle of passes through the point C.
For this circle, OC is diameter. Then the center is the midpoint of OC, which is .
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)25videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)46videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.65videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
Similar Questions
about to only mathematics
05:38View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
01:54View SolutionIf the circle x2+y2+2x+3y+1=0 cuts x2+y2+4x+3y+2=0 at AandB , then find the equation of the circle on AB as diameter.
03:25View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is08:10View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
04:31View SolutionThe line x+y=p meets the x- and y-axes at AandB , respectively. A triangle APQ is inscribed in triangle OAB,O being the origin, with right angle at Q.P and Q lie, respectively, on OBandAB . If the area of triangle APQ is 38th of the are of triangle OAB, the AQBQ is equal to (a)2(b) 23 (c) 13 (d)3
02:02View SolutionIf O is the origin and OPandOQ are the tangents from the origin to the circle x2+y2−6x+4y+8−0 , then the circumcenter of triangle OPQ is (3,−2) (b) (32,−1) (34,−12) (d) (−32,1)
03:21View SolutionA straight line through the origin O meets the parallel lines 4x+2y=9 and 2x+y+6=0 at points P and Q respectively. Then the point O divides the segement P Q in the ratio (1) 1:2 (2) 3:4 (3) 2:1 (4) 4:3
04:27View SolutionP is a point on positive x-axis, Q is a point on the positive y-axis and 'O' is the origin. If the line passing through P and Q is tangent to the curve y=3−x2 then find the minimum area of the triangle OPQ , is 3 (b) 4 (c) 5 (c) 6
03:58View SolutionIf the origin O and the points A ( 1, 2, 3), B (2, 3, 4) and P(x,y,z) are coplaner, then
02:36View SolutionThe line x+y=p meets the x- and y-axes at AandB , respectively. A triangle APQ is inscribed in triangle OAB,O being the origin, with right angle at Q.P and Q lie, respectively, on OBandAB . If the area of triangle APQ is 38th of the are of triangle OAB, the AQBQ is equal to (a)2(b) 23 (c) 13 (d)3
06:54View SolutionIf O is the origin and OPandOQ are the tangents from the origin to the circle x2+y2−6x+4y+8−0 , then the circumcenter of triangle OPQ is (3,−2) (b) (32,−1) (34,−12) (d) (−32,1)
04:09View SolutionThe locus of the midpoints of the chords of contact of x2+y2=2 from the points on the line 3x+4y=10 is a circle with center P. If O is the origin, then OP is equal to 2 (b) 3 (c) 12 (d) 13
10:05View SolutionIf tangents OQ and OR are dawn to variable circles having radius r and the center lying on the rectangular hyperbola xy=1 , then the locus of the circumcenter of triangle OQR is (O being the origin)
(a). xy=4 (b) xy=14 xy=1 (d) none of these03:48View SolutionIf S+O2→SO2,ΔH=−398.5kJ
SO2+12O2→SO3,ΔH=−98.7kJ,SO3+H2O→H2SO4,ΔH=−130.5kJ
H2+12O2→H2O,ΔH=−227.3kJ
If magnitude of enthalpy of formation of sulphuric acid at 298K is 95x, x= ?08:21View SolutionIf O is the origin and OP,OQ are the tangents from the origin to the circle x2+y2−6x+4y=8=0, then circum center of the triangle OPQ is
02:32View Solution
