Find the equations of the circles which pass through the origin and cut off chords of length a from each of the lines y=xandy=−xSolution in Tamil
The correct Answer is:x2+y2±√2ax=0 and x2+y2±√2ay=0
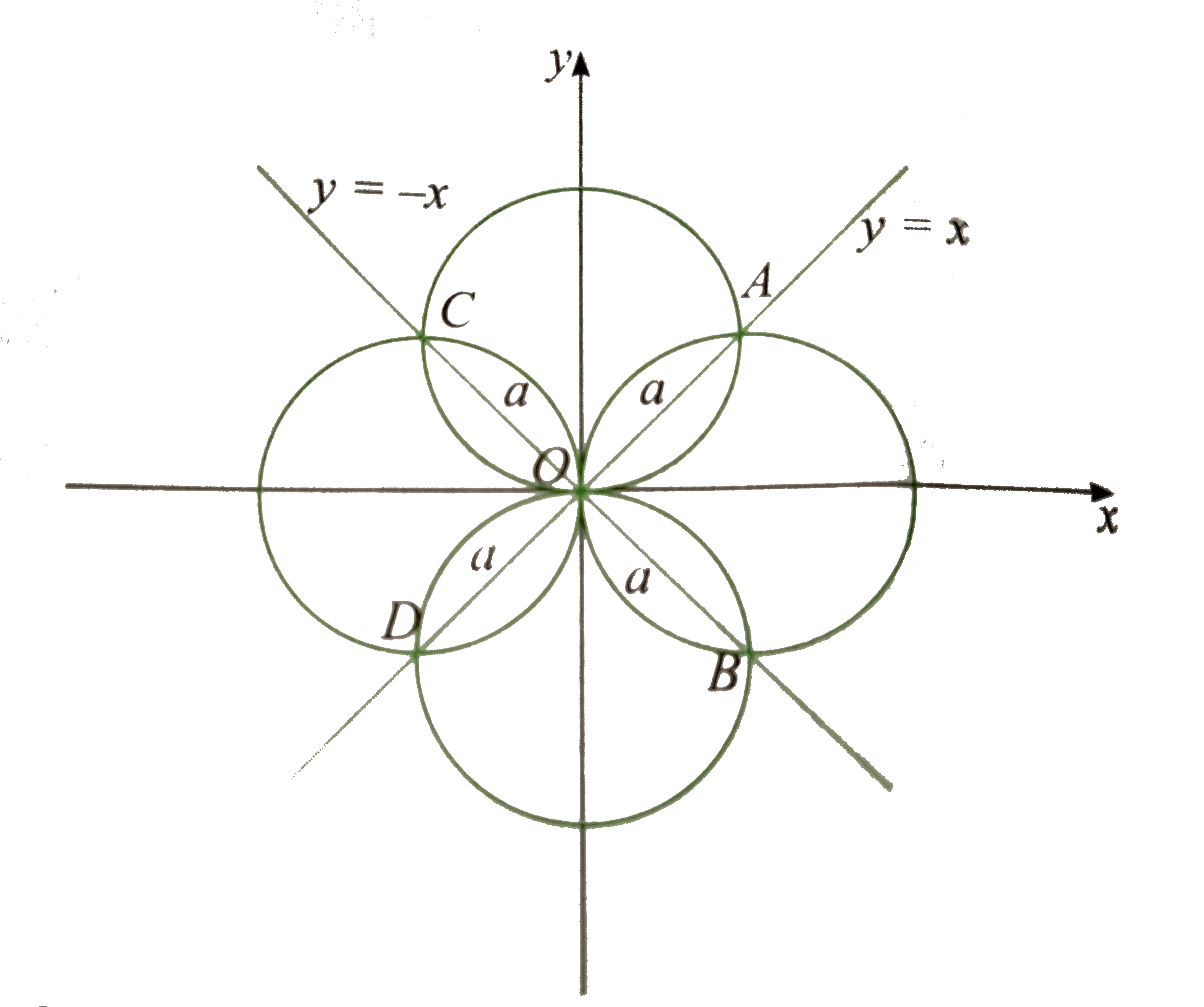
In the figure, length of chords OA and AB that cut off by the circles is a.
∴A≡(a√2,a√2) and B≡(a√2,−a√2), which are end points of diameters.
Therefore, the equation of circle is
(x−a√2)(x−a√2)+(y−a√2)(y+a√2)=0
or x2+y2−√2ax=0
Circles with AC and BD as diametere are given by x2+y2±√2ay=0
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.3
18 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.4
14 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.1
14 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
Find the angle between the two tangents from the origin to the circle (x−7)2+(y+1)2=25
View SolutionFind the equation of the tangent to the circle x2+y2+4x−4y+4=0 which makes equal intercepts on the positive coordinates axes.
View SolutionIf a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionIn how many ways can the letters of the word PENCIL be arranged so that (i) N is always next to E ? (ii) NandE are always together? .
View SolutionFind the equation of the circle which passes through the origin and cut off equal chords of √2 units from the lines y=xandy=−x.
View SolutionFind the equations of the circles which pass through the origin and cut off chords of length a from each of the lines y=xandy=−x
View SolutionFind the equation of the circle which passes through the origin and cuts off intercepts a and b respectively from x and y−axes.
View SolutionFind the locus of the centre of a circle which passes through the origin and cuts off a length 2l from the line x=c.
View SolutionFind the equations of the circles which pass through the origin and cut off equal chords of length √2 units on the straight lines y = x and y = - x .
View SolutionFind the equations to the circles which pass through the origin and cut off equal chords of length a unit from the lines y = x and y = -x.
View SolutionThe equation of the circle which passes through the origin and cuts off chords of length 2 from the lines x=y and x=-y is
View SolutionFind the equations of the circles which pass through the origin and cut off chords of length a from each of the lines y=xandy=−x
View SolutionFind the equation to the circle which passes through the origin and cut off equal chords of length 'a' from the straight lines y=xandy=−x .
View SolutionFind the equation of the circle which passes through the origin and cut off equal chords of √2 units from the lines y=xandy=−x.
View Solution
