A circle of radius 1 unit touches the positive x-axis and the positive y-axis at AandB , respectively. A variable line passing through the origin intersects the circle at two points DandE . If the area of triangle DEB is maximum when the slope of the line is m, then find the value of m−2Solution in Tamil
The equation of the circle is
(x−1)2+(y−1)2=1
or x2+y2−2x−2y+1=0 (1)
Let the equation of the variable straight line through origin be
y=mx (2)
This line intersects the cricle at two points D and E.
Distance of line from point B(0,1) is
BM=|m(0)−1|√1+m2=1√1+m2
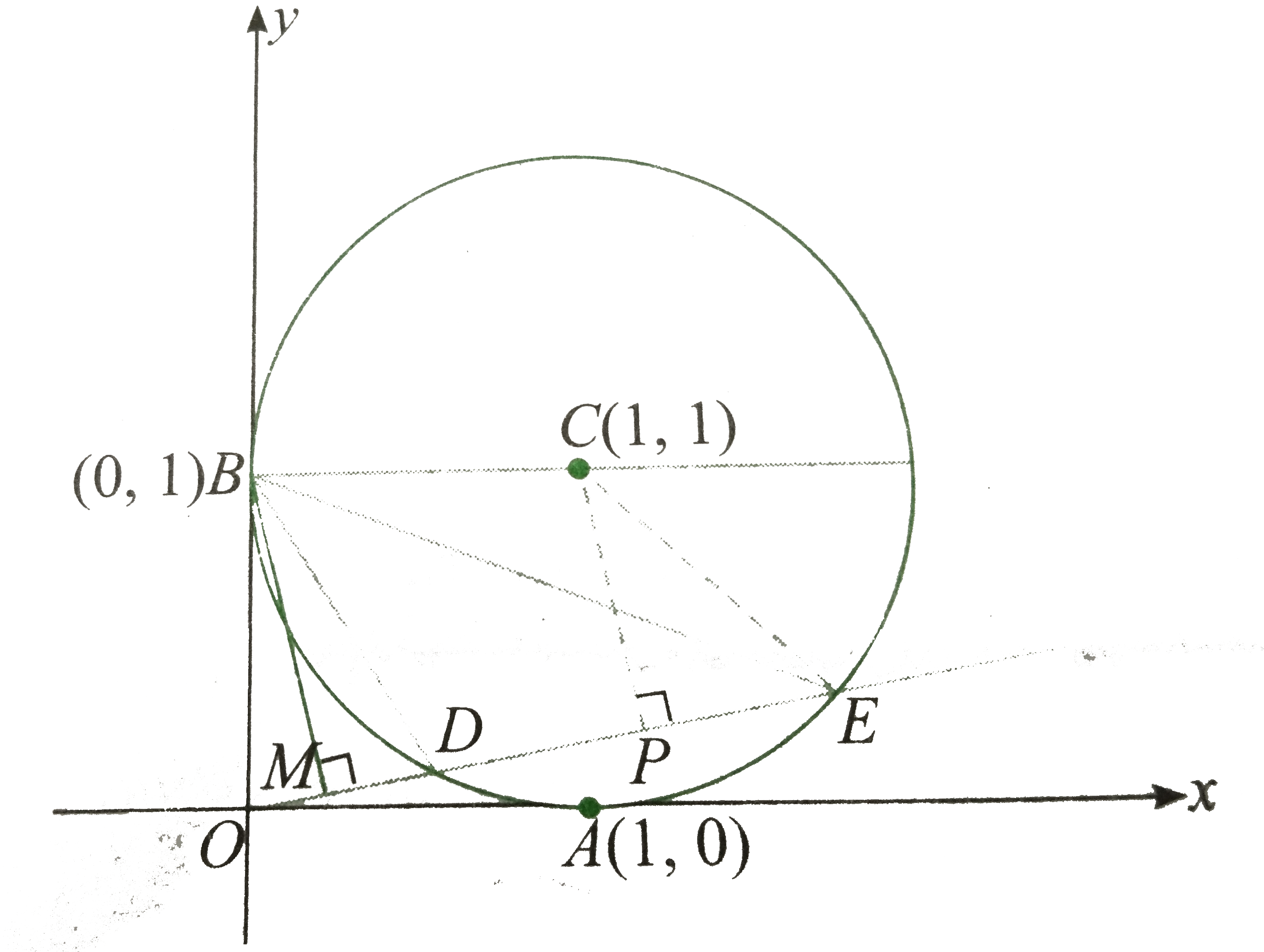
Also, CP=|m(1)−1|√1+m2=|m−1|√1+m2
∴DE=2PE=2√CE2−CP2=2√1−(m−1)21+m2=2√2m1+m2
∴Area of triangle DEB.
Δ=12BM×DE
=121√1+m2×2√2m1+m2=√2m1+m2
Differentiating Δ w.r.t. m, we get
dΔdm=√2⎡⎢⎣12√m(1+m2)−2m√m(1+m2)2⎤⎥⎦=1−3m2√2√m(1+m2)2
If dΔdm=0 , then m=1√m, whichi is point of maxima.
Therefore, area is maximum if m=1√3.
Topper's Solved these Questions
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionA circle of radius 1 unit touches the positive x-axis and the positive y-axis at AandB , respectively. A variable line passing through the origin intersects the circle at two points DandE . If the area of triangle DEB is maximum when the slope of the line is m, then find the value of m−2
View Solution(a) उस वृत्त का समीकरण ज्ञात कीजिए जो मूलबिंदु से होकर जाता है तथा x व y -अक्षों की धनात्मक दिशा से क्रमशः 6 तथा 8 इकाई के अन्तःखण्ड काटता है।
(b) उस वृत्त का समीकरण ज्ञात कीजिए जो मूलबिंदु से गुजरता है और x व y -अक्ष पर धन दिशा में क्रमशः 3 व 4 मात्रक का अन्तःखण्ड काटता है।
View SolutionLet A and B are two points on X -axis and y -axis respectively and circle passes , through A,B and O (origin).Tangent at origin is at a distance of 3 unit and 5 unit from point A and B respectively, then radius of circle is
View SolutionThe circle x2+y2=1 cuts the x-axis at PandQ. Another circle with center at Q and variable radius intersects the first circle at R above the x-axis and the line segment PQ at S. Find the maximum area of triangle QSR.
View SolutionA circle of radius 1 unit touches the positive x-axis and the positive y-axis at A and B , respectively. A variable line passing through the origin intersects the circle at two points D and E . If the area of triangle DEB is maximum when the slope of the line is m, then find the value of m−2
View SolutionA line passing through the origin O(0,0) intersects two concentric circles of radii aandb at PandQ, If the lines parallel to the X-and Y-axes through QandP, respectively, meet at point R, then find the locus of R.
View Solutionमूल बिन्दु से गुजरने वाले तथा x-अक्ष एवं y-अक्ष पर क्रमषः a तथा b लम्बाई के अन्तःखण्ड काटने वाले वृत्त का समीकरण ज्ञात कीजिये।
View SolutionDiametric form OF Circle || Different position OF circle ( Circle OF radius a & touching x axis,y axis ,origin, both axis)
View SolutionThe line passing through the extremity A of the major axis and extremity B of the minor axis of the ellipse x^(2)+9 y^(2)=9 meets the auxiliary circle at the point M. Then the area of the triangle with vertices A, M and the origin O is
View SolutionIf the radius of the circle passing through the origin and touching the line x+y=2 at (1,1) is r units, then the value of 3√2r is
View SolutionA circle of radius 1 unit touches the positive x-axis and the positive y-axis at Aa n dB , respectively. A variable line passing through the origin intersects the circle at two points Da n dE . If the area of triangle D E B is maximum when the slope of the line is m , then find the value of m^(-2)
View SolutionA line passing through the origin O(0,0) intersects two concentric circles of radii aandb at PandQ, If the lines parallel to the X-and Y-axes through QandP, respectively, meet at point R, then find the locus of R.
View Solution
