Let P be any moving point on the circle x2+y2−2x=1.AB be the chord of contact of this point w.r.t. the circle x2+y2−2x=0 . The locus of the circumcenter of triangle CAB(C being the center of the circle) is 2x2+2y2−4x+1=0 x2+y2−4x+2=0 x2+y2−4x+1=0 2x2+2y2−4x+3=0Solution in Tamil
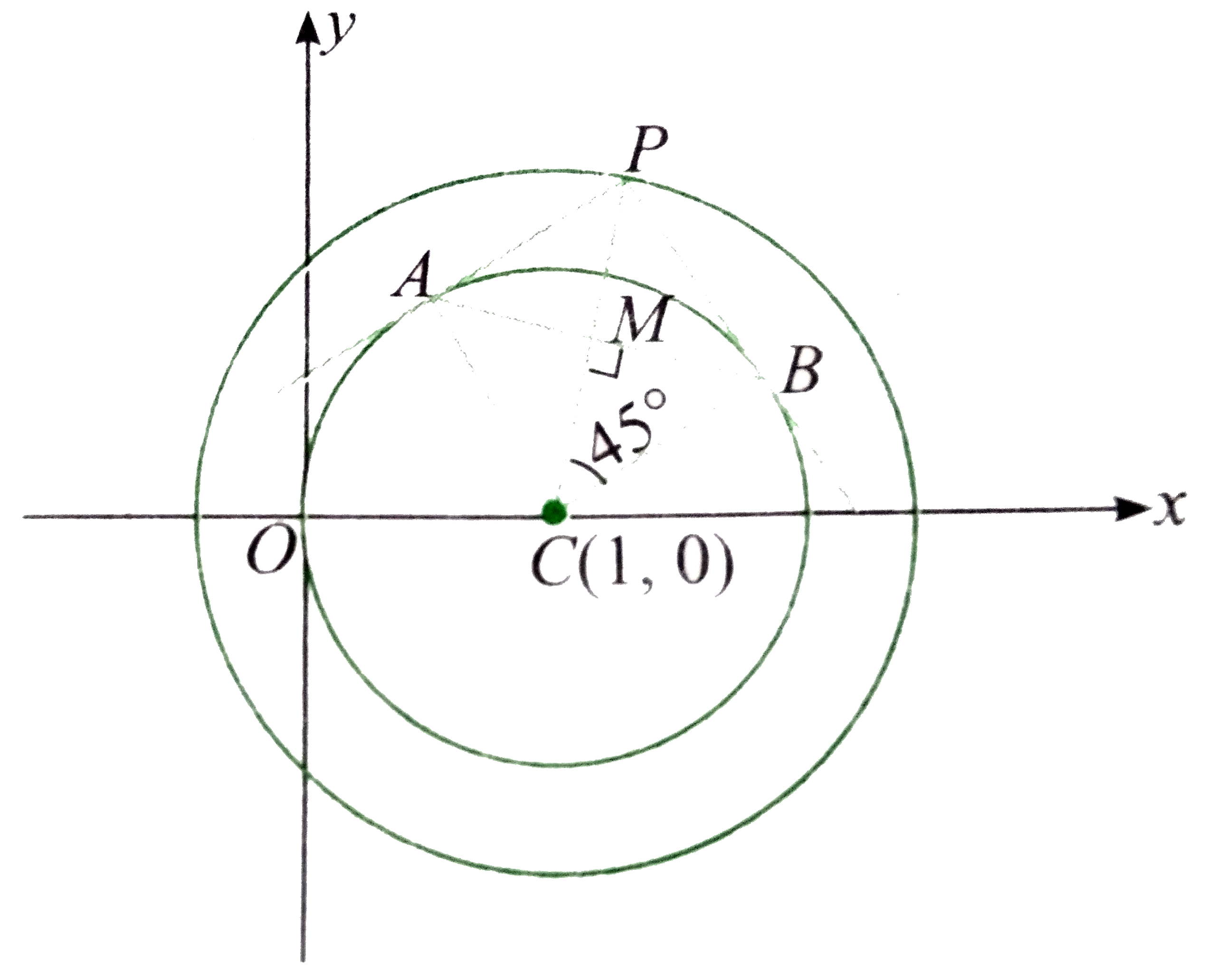
The two circles are
(x−1)2+y2=1 (1)
(x−1)2+y2=2 (2)
Clearly, the second circle is the director circle of the first circle.
∴∠AB=90∘
S, APBC is square.
Now, circumcentre of the right-angled triangle CAB will be midpoint of hypotenuse.
Let midpoint of AB be M(h,k).
Now, CM=CBsin45∘=1√2
So, (h−1)2+k2=12
Hence, locus of M is (x−1)2+y2=12
Topper's Solved these Questions
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionFind the length of the common chord of the circles x2+y2+2x+6y=0 and x2+y2−4x−2y−6=0
View SolutionLet P be any moving point on the circle x2+y2−2x=1.AB be the chord of contact of this point w.r.t. the circle x2+y2−2x=0 . The locus of the circumcenter of triangle CAB(C being the center of the circle) is 2x2+2y2−4x+1=0 x2+y2−4x+2=0 x2+y2−4x+1=0 2x2+2y2−4x+3=0
View Solutionवृत्तों x2+y2+2x+3y+1=0 व x2+y2+4x+3y+2=0 की उभयनिष्ठ जीवा की लम्बाई है-
View SolutionThe point of contact of the circle x2+y2+2x+2y+1=0andx2+y2−2x+2y+1=0
View SolutionThe length of the common chord of the circles
x2+y2+2x+3y+1=0,x2+y2+4x+3y+2=0 is
View SolutionThe radical center of the circles x2+y2−4x−6y+5=0,x2+y2−2x−4y−1=0,x2+y2−6x−2y=0.
View Solutionवृत्तों x2+y2+2x+3y+1=0 तथा x2+y2+4x+3y+2=0की उभयनिष्ठ जीवा की लम्बाई है
View SolutionLength of the common chord of the circles : x2+y2+2x+6y=0 and x2+y2−4x−2y−6=0 is :
View SolutionShow that the circle x2+y2+4x+4y−1=0 bisects the circumference of the circle x2+y2+2x−3=0 .
View SolutionThe common tangent at the point of contact of the two circles x2+y2−4x−4y=0,x2+y2+2x+2y=0 is
View SolutionFind the length of the common chord of the circles x2+y2+2x+6y=0 and x2+y2−4x−2y−6=0
View SolutionLet P be any moving point on the circle x2+y2−2x=1.AB be the chord of contact of this point w.r.t. the circle x2+y2−2x=0 . The locus of the circumcenter of triangle CAB(C being the center of the circle) is a.2x2+2y2−4x+1=0 b.x2+y2−4x+2=0 c.x2+y2−4x+1=0 d.2x2+2y2−4x+3=0
View Solution
