Tangents are drawn to the circle x2+y2=a2 from two points on the axis of x, equidistant from the point (k,0). Show that the locus of their intersection is ky2=a2(k−x).Solution in Tamil
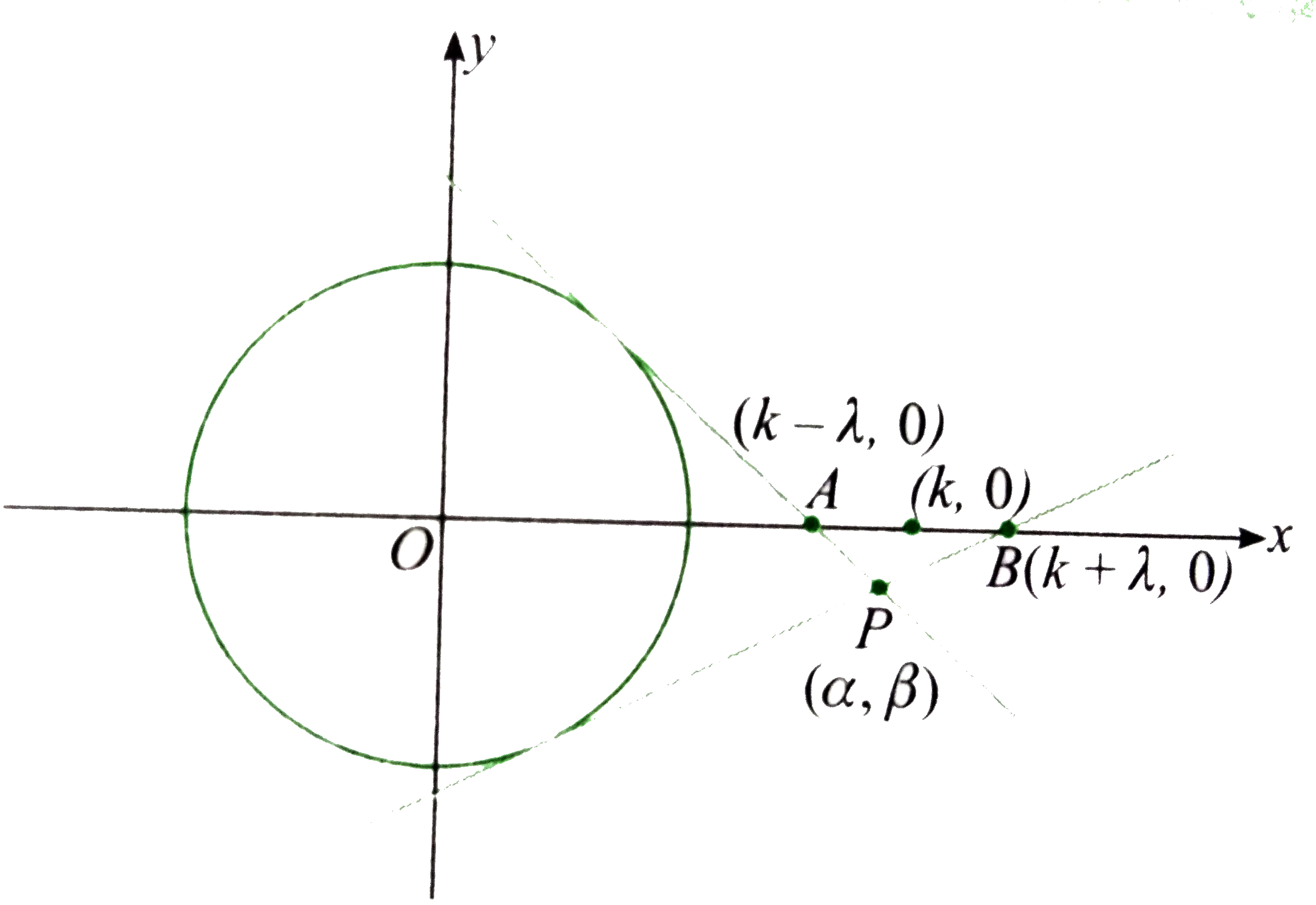
As shown in figure , point A and B are equidistant from point (k,0).
Tangents drawn from point A and B intersect at point P(α,β).
Equation of pair of tangents from point P is
(x2+y2−a2)(α2+β2−a2)=(αx+βy−a2)2 (Using T2=SS1)
This equation is satisfied by points A and B .
∴((k−λ)2−a2)(α2+β2−a2)=(α(k−λ)−a2)2 (1)
and ((k+λ)2−a2)(α2+β2−a2)=(α(k+λ)−a2)2 (2)
Subtracting (1) and (2) , we get
(α2+β2−a2)(4kλ)=[(k+λ)α−a2+(k−λ)α−a2][(k+λ)α−(k−λ)α]=[2(kα−a2)][2λα]=4λα[kα−a2]
⇒k(α2+β2−a2)=kα2−a2α
⇒kβ2=a2(k−α)
Hence, the locu is ky2=a2(k−x)
Topper's Solved these Questions
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionThe locus of the point of intersection of the two tangents drawn to the circle x^(2)+y^(2)=a^(2) which include are angle alpha is
View SolutionTangents are drawn to the circle x2+y2=a2 from two points on the axis of x, equidistant from the point (k,0). Show that the locus of their intersection is ky2=a2(k−x).
View SolutionA tangent is drawn to each of the circles x2+y2=a2 and x2+y2=b2. Show that if the two tangents are mutually perpendicular, the locus of their point of intersection is a circle concentric with the given circles.
View SolutionIf chord of contact of the tangent drawn from the point (a,b) to the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 touches the circle x^(2)+y^(2)=k^(2), then find the locus of the point (a,b).
View SolutionNumber of integral value(s) of k for which no tangent can be drawn from the point (k,k+2) to the circle x2+y2=4 is :
View SolutionThe locus of the feet of the perpendicular drawn from the point (a,0) on tangent to the circle x2+y2=a2 is
View SolutionThe length of the tangent from the point (-1,1) to the circle x2+y2−4x+k=0 equal to 2 then k=
View SolutionThe value of k for which two tangents can be drawn from (k,k) to the circle x^2+y^2+2x+2 y-16=0
View Solutionएक नियत बिंदु (h,k) से वृत्त x2+y2=r2 पर एक छेदक रेखा (secant) खींची जाती है। दिखाइए की वृत्त पर खींची गई छेदक रेखाओं के मध्य-बिंदु का बिन्दुपथ x2+y2=hx+ky है।
View SolutionTangents are drawn to the circle x2+y2=a2 from two points on the axis of x, equidistant from the point (k,0). Show that the locus of their intersection is ky2=a2(k−x).
View SolutionA tangent is drawn to each of the circles x2+y2=a2 and x2+y2=b2. Show that if the two tangents are mutually perpendicular, the locus of their point of intersection is a circle concentric with the given circles.
View Solutionयदि बिन्दु (1,2) से वृत्तों x2+y2+x+y−4=0 तथा 3x2+3y2−x−y+k=0 पर खींची गयी स्पर्श रेखाओं की लम्बाइयों का अनुपात 4:3 हो, तो k =
View Solution
