If θ is the angle between the two radii (one to each circle) drawn from one of the point of intersection of two circles x2+y2=a2 and (x−c)2+y2=b2, then prove that the length of the common chord of the two circles is 2absinθ√a2+b2−2abcosθSolution in Tamil
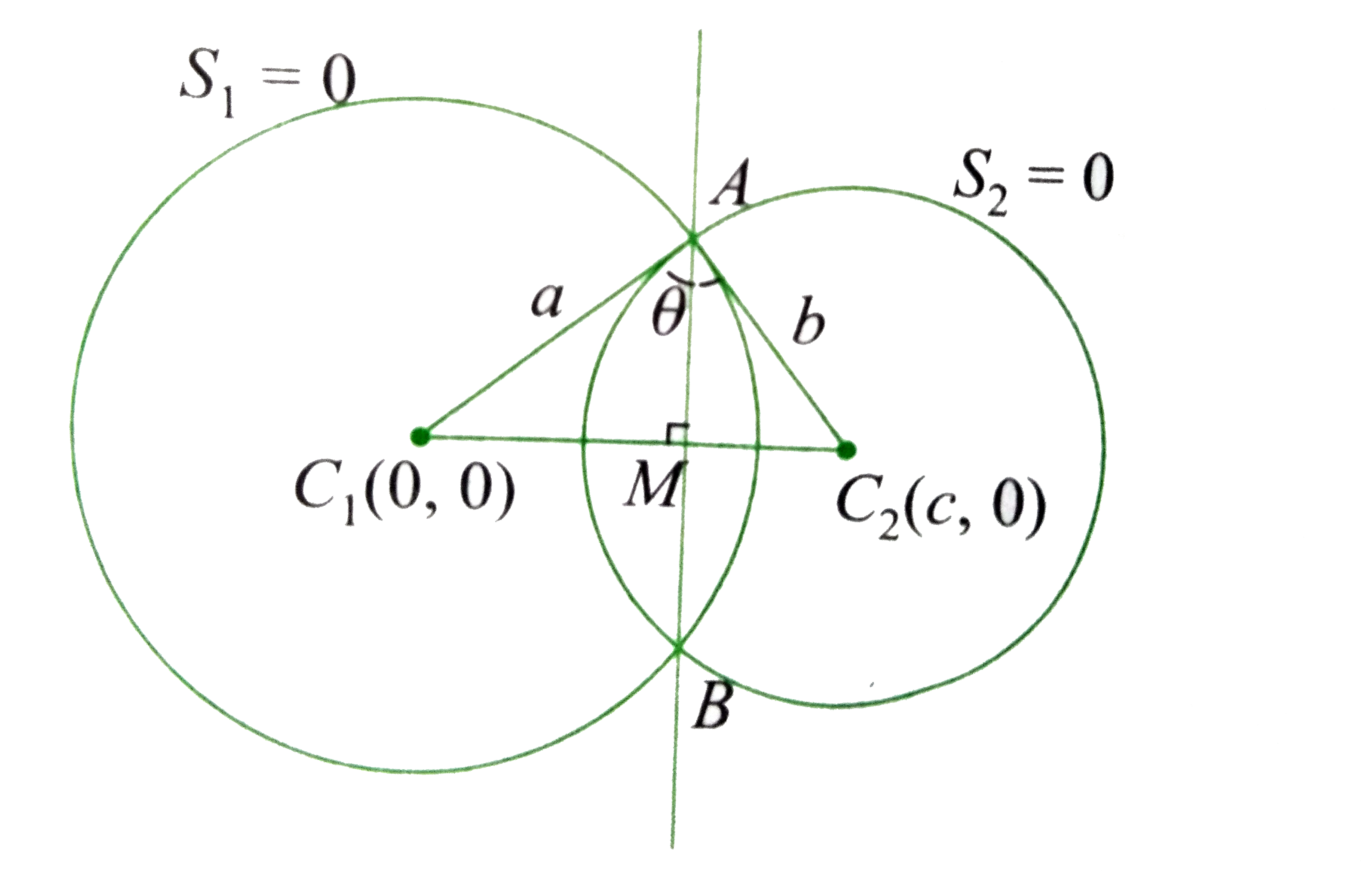
From the figure,
cosθ=a2+b2−c22ab
∴c=√a2+b2−2abcosθ=C1C2
Area of triangle C1AC2=12absinθ=12AM×C2C2
∴AM=absinθ√a2+b2−2abcosθ
∴ Length of common chord, AB=2AM=2absinθ√a2+b2−2abcosθ
Topper's Solved these Questions
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionIf θ is the angle between the two radii (one to each circle) drawn from one of the point of intersection of two circles x2+y2=a2 and (x−c)2+y2=b2, then prove that the length of the common chord of the two circles is 2absinθ√a2+b2−2abcosθ
View SolutionA tangent is drawn to each of the circles x2+y2=a2 and x2+y2=b2. Show that if the two tangents are mutually perpendicular, the locus of their point of intersection is a circle concentric with the given circles.
View SolutionIf two tangents are drawn from a point to the circle x2+y2=32 to the circle x2+y2=16, then the angle between the tangents is
View Solutionसिद्ध कीजिए की उस वृत्त के केन्द्र का बिन्दुपथ जो x-अक्ष से दी हुई लम्बाई 2a की जीवा कटती है और y-अक्ष पर मूलबिन्दु से b दूरी पर किसी दिए हुए बिन्दु से होकर जाता है, x2−2by+b2=a2 है।
View SolutionThe equation of the common chord of the two circles
(x−a)2+(y−b)2=c2,(x−b)2+(y−a)2=c2 is
View SolutionThe equation of the common chord of the two circles
(x−a)2+(y−b)2=c2,(x−b)2+(y−a)2=c2 is
View SolutionThe lengthk of the equation chord of the two circles (X−a)2+y2=a2 and x2+(y−b)2=b2 is
View SolutionThe length of the common chord of the two circles (x−a)2+y2=a2 and x2+(y−b)2=b2 is
View SolutionThe length of the common chord of the two circles (x−a)2+(y−b)2=c2,(x−b)2+(y−a)2=c2 is
View SolutionIf θ is the angle between the two radii (one to each circle) drawn from one of the point of intersection of two circles x2+y2=a2 and (x−c)2+y2=b2, then prove that the length of the common chord of the two circles is 2absinθ√a2+b2−2abcosθ
View SolutionA tangent is drawn to each of the circles x2+y2=a2 and x2+y2=b2. Show that if the two tangents are mutually perpendicular, the locus of their point of intersection is a circle concentric with the given circles.
View SolutionIf two tangents are drawn from a point to the circle x2+y2=32 to the circle x2+y2=16, then the angle between the tangents is :
View Solution
