The circle does not touch or intersect the coordinate axes, and the point (1, 4) is inside the circle. Find the range of value of Solution in Tamil
The equation of the circle is
(1)
whose center is C(3,5) and radius
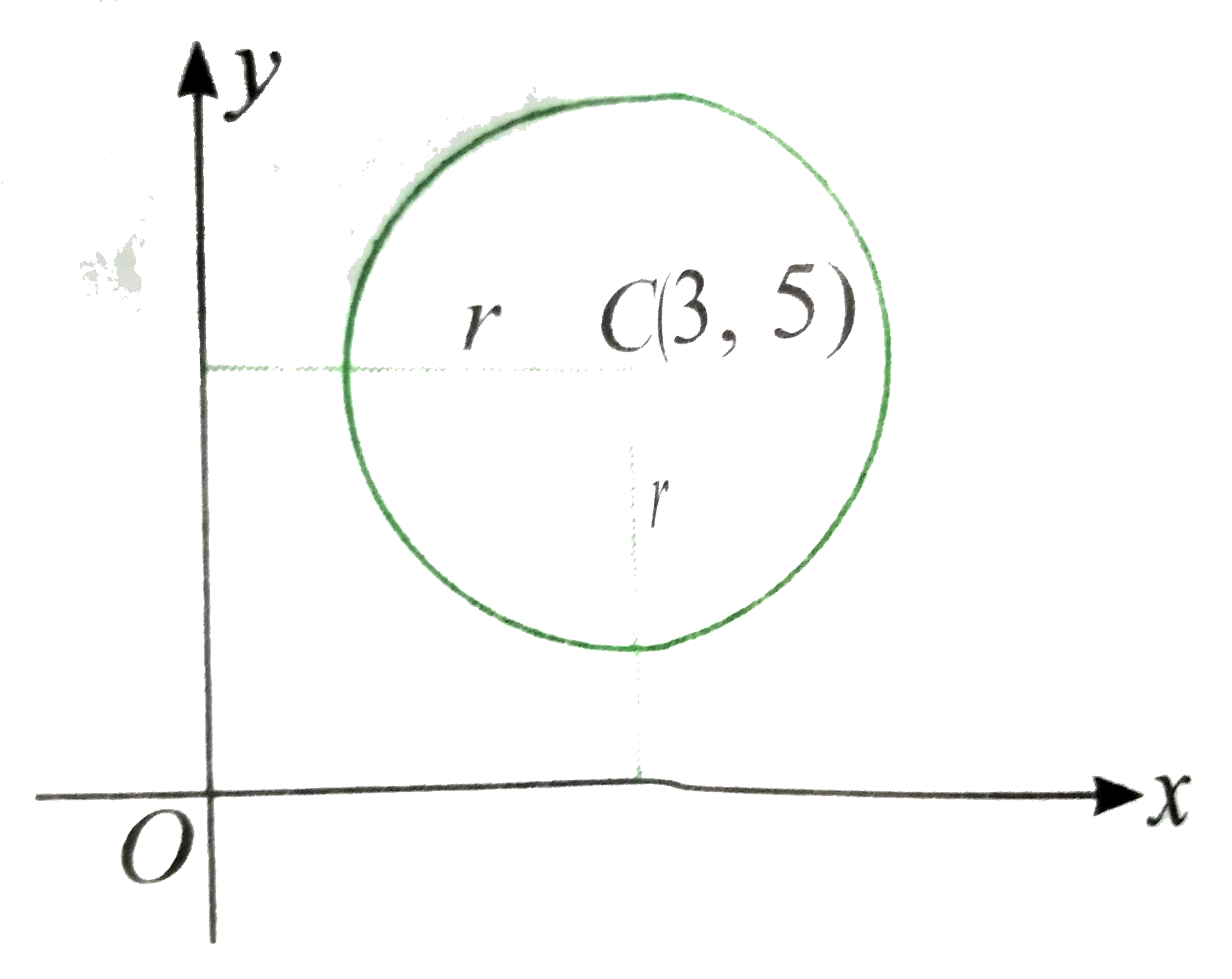
If the circle does not touch or intersect the x-axis, then radius
coordinate of center C
or
or
or (2)
Also, if the circle does not touch or intersect the y-axis, then the radius
coordinate of center C
or
or
or (3)
If the point (1,4) is inside the circle, then
Its distance from center
or
or
or (4)
Now, all the conditions (2),(3), and (4) are satisfied if which is the required range of the values of k.
Topper's Solved these Questions
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionFind the coordinates of point equidistant from axes and lying on the circle x^(2)+y^(2)-6x-2y+6=0
View SolutionThe circle x^(2)+y62-6x-10y+c=0 does not touch and intersect the coordinate axes and the point (1,4) is inside the circle.find the set of values of c.
View SolutionThe circle x2+y2−6x−10y+k=0 does not touch or intersect the coordinate axes, and the point (1, 4) is inside the circle. Find the range of value of k.
View SolutionIf the circle x^(2)+y^(2)-4x-6y+k=0 does not touch or intersect the axes and the point (2,2) liel inside the circle,then k can lie in the interval/ntervals
View SolutionFind the coordinates of points equidistant from the axes and lying on the circle x2+y2−6x−2y+6=0.
View SolutionThe circle x2+y2−6x−10y+λ=0 does not touch or intersect the coordinate axes and the point (1,4) is inside the circle. Find the range of values of λ.
View SolutionThe circle x2+y2−6x−10y+k=0 does not touch or intersect the x-axis and the point (1, 4) lies inside the circle, then:
View Solutionx2+y2−6x−2y+6=0 বৃত্তের ওপর অবস্থিত ও অক্ষ দুটি থেকে সমদূরবর্তী বিন্দুসমূহের স্থানাঙ্ক নির্ণয় করো।
View SolutionThe circle x2+y2−6x−10y+k=0 does not touch (or ) Intersects the coordinate axes and the point (1,4) lies inside the circle then limits of k are.
View SolutionIf a point (1,4) lies inside the circle x2+y2−6x−10y+p=0 and the circle does not touch or intersect the coordinate axes , then the set of all possible values of p is the interval.
View SolutionIf the line y=√3x+k touches the circle x2+y2=16, then find the value of k.
View SolutionThe circle x2+y2−6x−10y+k=0 does not touch or intersect the coordinate axes, and the point (1, 4) is inside the circle. Find the range of value of k.
View Solution
