Tangents are drawn to from the point Then find the equation of the circumcircle of triangle Solution in Tamil
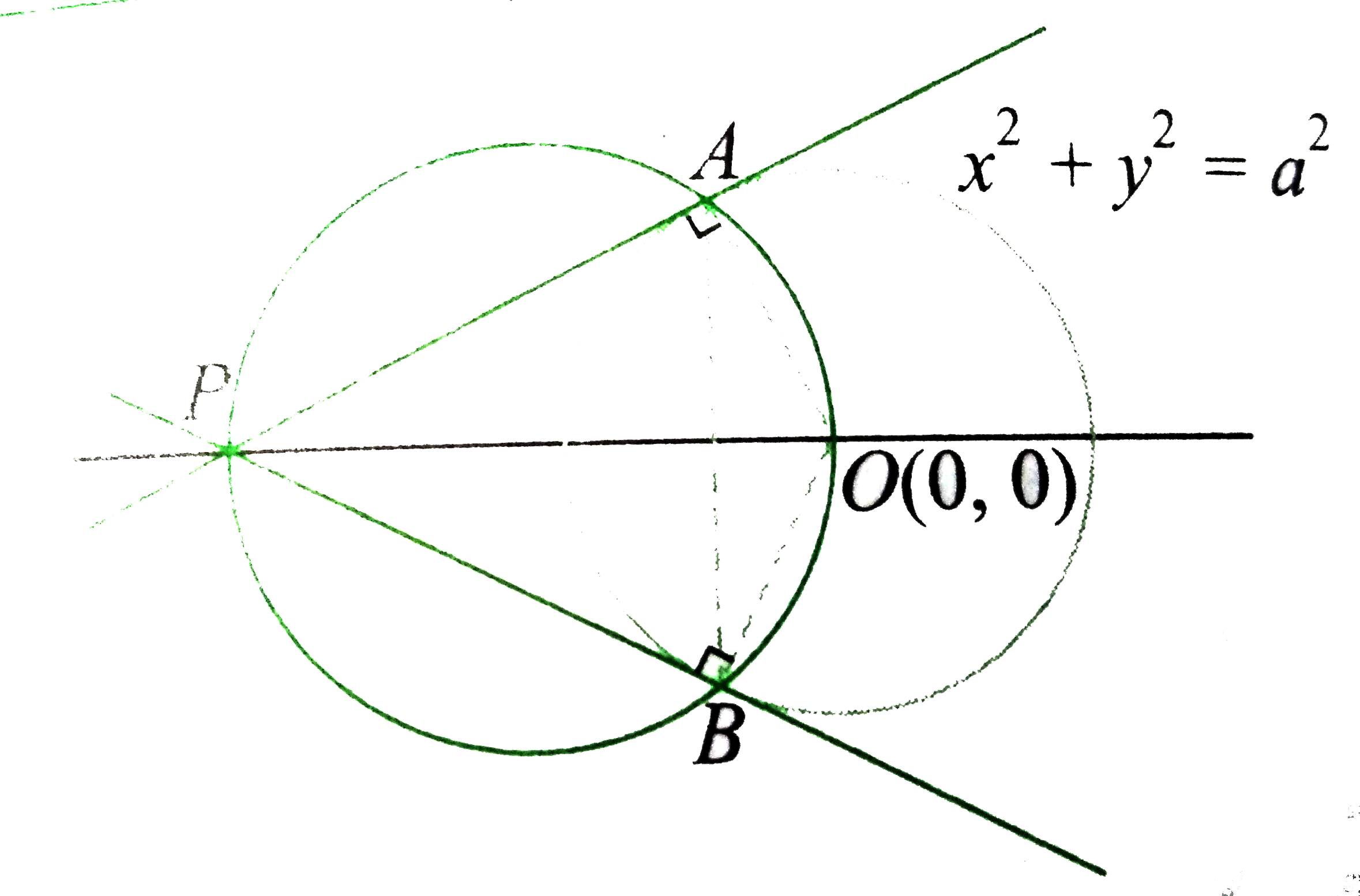
From the figure, clearly the points O,A,P and B are concyclic and OP is diameter of the circle.
Thus, equation of circumcircle of triangle PAB is
or
Topper's Solved these Questions
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionTangent PQ and PR are drawn to the circle x2+y2=a2 from the pint P(x1,y1). Find the equation of the circumcircle of ΔPQR.
View SolutionTangents PAandPB are drawn to x2+y2=a2 from the point P(x1,y1). Then find the equation of the circumcircle of triangle PAB.
View SolutionTangent PAandPB are drawn from the point P on the directrix of the parabola (x−2)2+(y−3)2=(5x−12y+3)2160 . Find the least radius of the circumcircle of triangle PAB.
View SolutionTangents PQandPR are drawn at the extremities of the chord of the ellipse x216+y29=1 , which get bisected at point P(1,1). Then find the point of intersection of the tangents.
View SolutionIf tangents PQandPR are drawn from a variable point P to thehyperbola x2a2−y2b2=1,(a>b), so that the fourth vertex S of parallelogram PQSR lies on the circumcircle of triangle PQR , then the locus of P is x2+y2=b2 (b) x2+y2=a2 x2+y2=a2−b2 (d) none of these
View SolutionIf tangents PQandPR are drawn from a variable point P to thehyperbola x2a2−y2b2=1,(a>b), so that the fourth vertex S of parallelogram PQSR lies on the circumcircle of triangle PQR , then the locus of P is (a) x2+y2=b2 (b) x2+y2=a2 (c) x2+y2=a2−b2 (d) none of these
View SolutionTangent PAandPB are drawn from the point P on the directrix of the parabola (x−2)2+(y−3)2=(5x−12y+3)2160 . Find the least radius of the circumcircle of triangle PAB.
View SolutionTangents PAandPB are drawn to x2+y2=a2 from the point P(x1,y1). Then find the equation of the circumcircle of triangle PAB.
View SolutionIf from a point P, tangents PQandPR are drawn to the ellipse x22+y2=1 so that the equation of QR is x+3y=1, then find the coordinates of P.
View SolutionIf from a point P(a,b,c) prpendiculars PAandPB are drawn to yzandzx−planes, find the eqution of th plane OAB.
View SolutionIf from a point P(a,b,c) perpendiculars PAandPB are drawn to YZandZX−planes find the vectors equation of the plane OAB.
View SolutionTangents are drawn to x2+y2=16 from the point P(0,h). These tangents meet the x−aξs at AandB . If the area of triangle PAB is minimum, then h=12√2 (b) h=6√2 h=8√2 (d) h=4√2
View Solution
