A point moves such that the sum of the squares of its distances from the two sides of length ‘a’ of a rectangle is twice the sum of the squares of its distances from the other two sides of length b. The locus of the point can be:Solution in Tamil
a circle
an ellipse
a hyperbola
a pair of lines
The correct Answer is:C, D
Let the two sides of the rectangle lie along x-axis and y-axis.
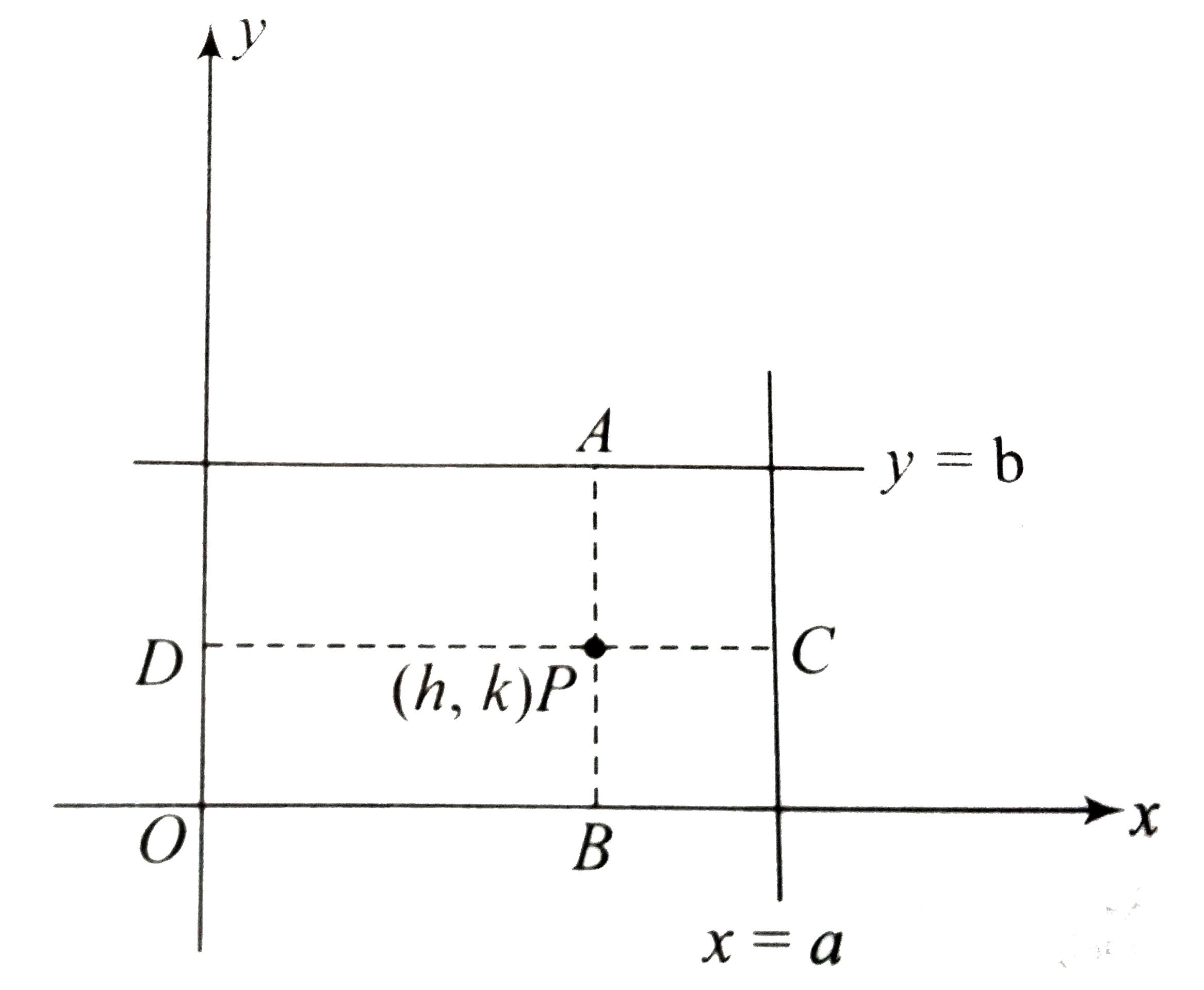
Let point P be (h,k)
Given that
(PA)2+(PB)2=2(PC2+PD2)
⇒k2−(k−b)6(2)=2(h2+(a−h)2)
⇒2k2−2kb+b2=4h2−4ah+2a2
Replacing h by x and k by y
⇒2y2−2by+b2=4x2−4ax+2a2
or 2(y2−by)+b2=4(x2−ax)+2a2
or 4(x−a2)2−2(y−b2)2=b22−a2
Hence it is a hyperbola if b22−a2≠0
or pair of lines if b22−a∘=0
Similar Questions
The point P moves such that the sum of the squares of its distances from two fixed points A(a,0)andB(−a,0) is constant and equal to 6a2. The locus of P is
View SolutionThe locus of a point, which moves in such a way that the sum of the squares of its distances from the four sides of a square is consant (=2c2) is
View Solutionकिसी चर बिंदु की दो स्थिर बिंदुओं से दूरियों के वर्गों का योग एक अचर राशि है । उसके बिन्दुपथ का समीकरण ज्ञात कीजिए ।
View SolutionA point moves so that the sum of squares of its distances from the points (1,2) and (-2,1) is always 6. then its locus is
View SolutionThe sum of the squares of the distances of a moving point from two fixed points (a,0) and (−a,0) is equal to a constant quantity 2c2. Find the equation to its locus.
View SolutionA point moves such that the sum of the squares of its distances from the two sides of length ‘a’ of a rectangle is twice the sum of the squares of its distances from the other two sides of length b. The locus of the point can be:
View Solutionएक बिन्दु इस प्रकार गति करता है कि इसकी एक इकाई लम्बाई भुजा वाले वर्ग की भुजाओं से दूरियों के वर्गों का योग 9 रहता है, तो इस बिन्दु का बिन्दुपथ होगा
View SolutionThe point P moves such that the sum of the squares of its distances from two fixed points A(a,0),B(−a,0) is 8a2 the locus of P is
View Solution
