Tangents PAandPB are drawn to the circle x2+y2=8 from any arbitrary point P on the line x+y=4. The locus of mid-point of chord of contact AB isSolution in Tamil
x2+y2−2x−2y=0
x2+y2+2x+2y=0
x2+y2−2x+2y=0
x2+y2+2x−2y=0
The correct Answer is:A
Let P(a,4−a).
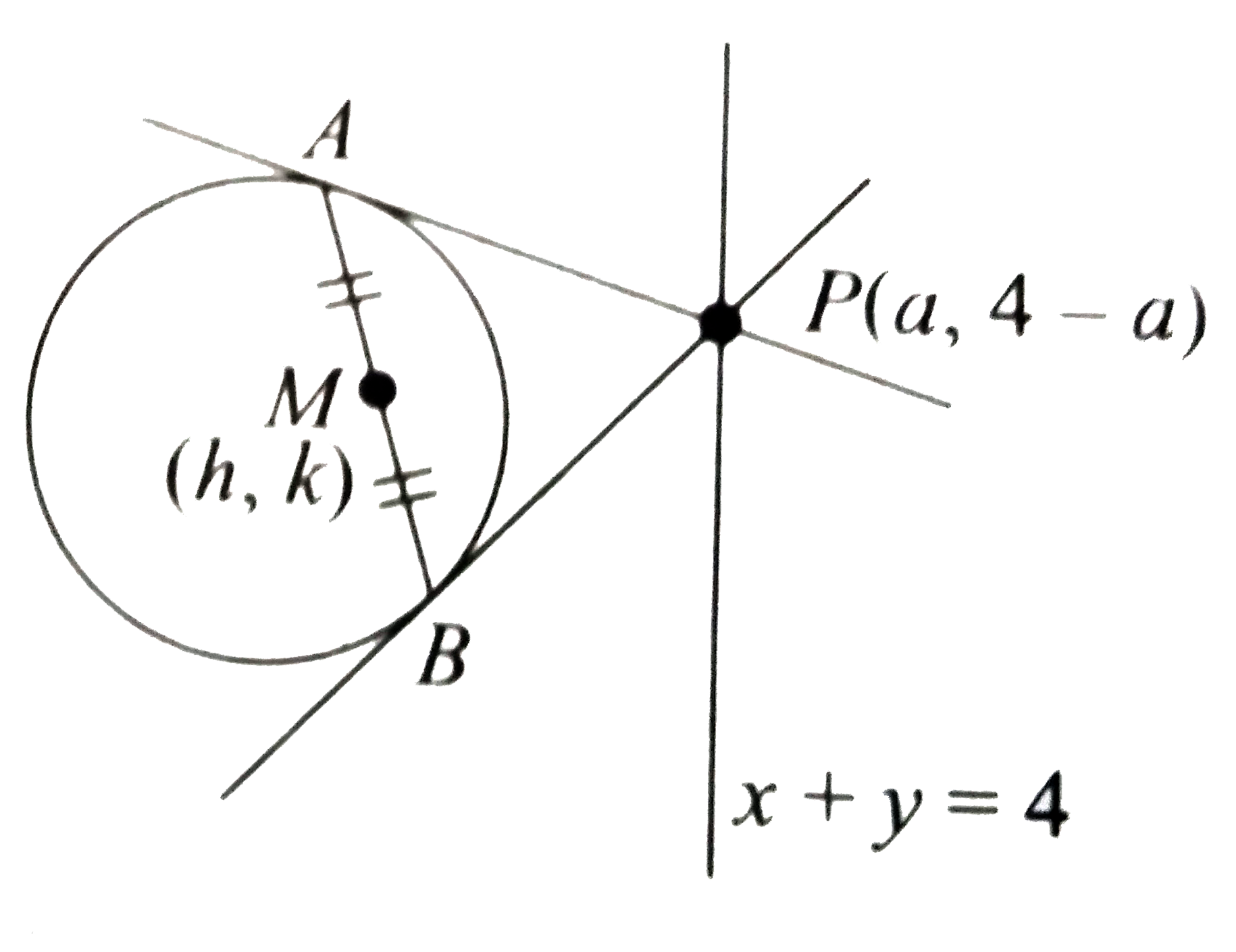
The equation of chord of contact AB is
xa+y(4−a)=8 (i)
Also, equation of chord AB whose mid-points is M(h,k) is
hx+ky=h2+k2 (ii) (using T=S1)
Since (i) and (ii) are identical, on comparing the coefficients, we get
ah=4−ak=8h2+k2=a+4−ah+k=4h+k
⇒4(h2+k2)=8(h+k)
Hence, locus of M(h,k) is x2+y2−2x−2y=0.
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type
9 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
6 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Advanced Previous Year
14 Videos
Similar Questions
The line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
View SolutionIn the diagram as shown, a circle is drawn with centre C(1, 1) and radius I and a line L. The line Lis tangential to the circle at Q. Further L meet the y-axis at R and the x-axis at Pis such a way that the angle OPQ equals θ where 0<θ<π2 The coordinates of Q are
View SolutionFind the derivative of y=ln(cosx2).
View SolutionLet z=x+iy be a complex number where xandy are integers. Then, the area of the rectangle whose vertices are the roots of the equation zz3+zz3=350 is 48 (b) 32 (c) 40 (d) 80
View SolutionTangents PA and PB are drawn to the circle x^(2)+y^(2)=8 from any arbitrary point P on the line x+y=4. The locus of mid-point of chord of contact AB is
View SolutionTangents are drawn from points on the line x+2y=8 to the circle x^(2)+y^(2)=16. If locus of mid-point of chord of contacts of the tangents is a circles S, then radius of circle S will be
View SolutionA tangent is drawn at any point P(t) on the parabola y^(2)=8x and on it is taken a point Q(alpha,beta) from which pair of tangent QA and QB are drawn to the circle x^(2)+y^(2)=4. The locus of the point of concurrency of the chord of contact AB of the circle x^(2)+y^(2)=4 is
View SolutionTangents PA and PB are drawn to parabola y2=4x from any arbitrary point P on the line x+y=1.
Then vertex of locus of midpoint of chord AB is
View SolutionThe tangents PA and PB are drawn from any point P of the circle x2+y2=2a2 to the circle x2+y2=a2. The chord of contact AB on extending meets again the first circle at the points A' and B'. The locus of the point of intersection of tangents at A' and B' may be given as
View SolutionPA and PB are tangents drawn from a point P to the ellipse x2a2+y2b2=1. The area of the triangle formed by the chord of contact AB and axes of co-ordinates is constant. Then locus of P is:
View SolutionFrom points on the circle x2+y2=a2 tangents are drawn to the hyperbola x2−y2=a2. Then, the locus of mid-points of the chord of contact of tangents is:
View SolutionA variable point P is chosen on the straight line x + y = 4 and tangents PA and PB are drawn from it to circle x2+y2=1 . Then the position of P for the smallest length of chord of contact AB is
View SolutionFrom the point P(2, 3) tangents PA,PB are drawn to the circle x2+y2−6x+8y−1=0. The equation to the line joining the mid points of PA and PB is
View Solutionबिंदु P से वृत x2+y2=4 पर स्पर्श रेखाऐं PA एवं PB
इस प्रकार खींची गई है की त्रिभुज PAB एक समबाहु त्रिभुज है
तो P का बिन्दुपथ होगा।
View SolutionTangents PA and PB are drawn to parabola y2=4x from any arbitrary point P on the line x+y=1.
Then vertex of locus of midpoint of chord AB is
View Solution