A circle of radius 2 has its centre at (2, 0) and another circle of radius 1 has its centre at (5, 0). A line is tangent to the two circles at point in the first quadrant. The y-intercept of the tangent line isSolution in Tamil
√2
2√2
3√2
4√2
The correct Answer is:B
12=a−5a−2⇒a=8
Thus, equation of line is y=m(x−8)
Now, this line touches the circle.
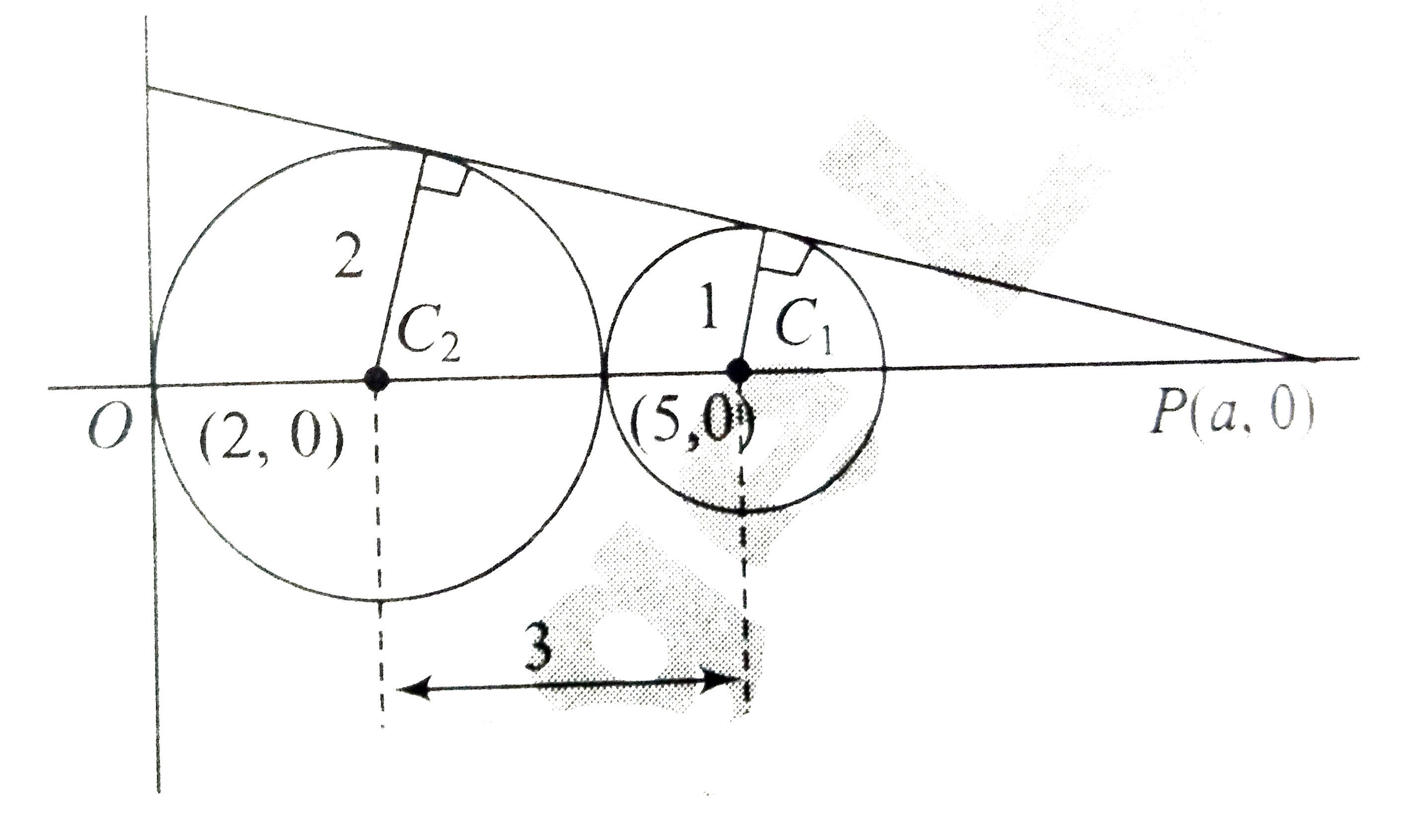
∴∣∣∣6m√1+m2∣∣∣=2
⇒9m2=1+m2
∴m=−1√8
⇒ y-intercept =√8=2√2.
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type
9 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
6 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Advanced Previous Year
14 Videos
Similar Questions
The line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
View SolutionIn the diagram as shown, a circle is drawn with centre C(1, 1) and radius I and a line L. The line Lis tangential to the circle at Q. Further L meet the y-axis at R and the x-axis at Pis such a way that the angle OPQ equals θ where 0<θ<π2 The coordinates of Q are
View SolutionFind the derivative of y=ln(cosx2).
View SolutionLet z=x+iy be a complex number where xandy are integers. Then, the area of the rectangle whose vertices are the roots of the equation zz3+zz3=350 is 48 (b) 32 (c) 40 (d) 80
View SolutionThe line 2x-y+1=0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x-2y=4. The radius of the circle is :
View SolutionThe line 2x-y+1=0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x-2y=4 The radius of the circle is:
View SolutionA circle of radius 2 has its centre at (2,0) and another circle of radius 1 has its centre at (5, 0).A line is tangent to the two circles at point in the first quadrant.The y-intercept of the tangent line is
View SolutionThe line 2x-y+1=0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x-2y=4. The radius of the circle is
View SolutionA circle touches the line y=x at the point (2,2) and has it centre on y-axis, then square of its radius is
View SolutionIF the locus of the point of intersection of two perpendicular tangents to a hyperbola x225−y216=1 is a circle with centre (0, 0), then the radius of a circle is
View SolutionIf the line x+3y=0 is tangent at (0,0) to the circle of radius 1, then the centre of one such circle is
View SolutionIf the line x+3y=0 is the tangent at (0,0) to the circle of radius 1, then the centre of one sum circle is
View SolutionThe line 2x−y+1=0 is tangent to the circle at the point (2, 5) and the centre of the circle lies on x−2y=4. The square of the radius of the circle is
View SolutionThe line y=x is a tangent at (0,0) to a circle of radius is 1, then centre of the circle is
View SolutionA circle of radius 2 has its centre at (2, 0) and another circle of radius 1 has its centre at (5, 0). A line is tangent to the two circles at point in the first quadrant. The y-intercept of the tangent line is
View SolutionIf lines 3x-4y+4=0 And 6x-8y-7=0 If a circle has tangent lines, the radius of the circle is
View Solution
