The locus of the foot of the perpendicular from the origin on each member of the family (4a+3)x−(a+1)y−(2a+1)=0Solution in Tamil
(2x−1)2+4(y+1)2=5
(2x−1)2+(y+1)2=5
(2x+1)2+4(y−1)2=5
(2x−1)2+4(y−1)2=5
The correct Answer is:C
Given family of lines is (4a+3)x−(a+1)y−(2a+1)=0
or (3x−y−1)+a(4x−y−2)=0
Family of lines passes through the fixed point P which is the intersection of
3x−y=1 and 4x−y=2
Solving we get P(1,2).
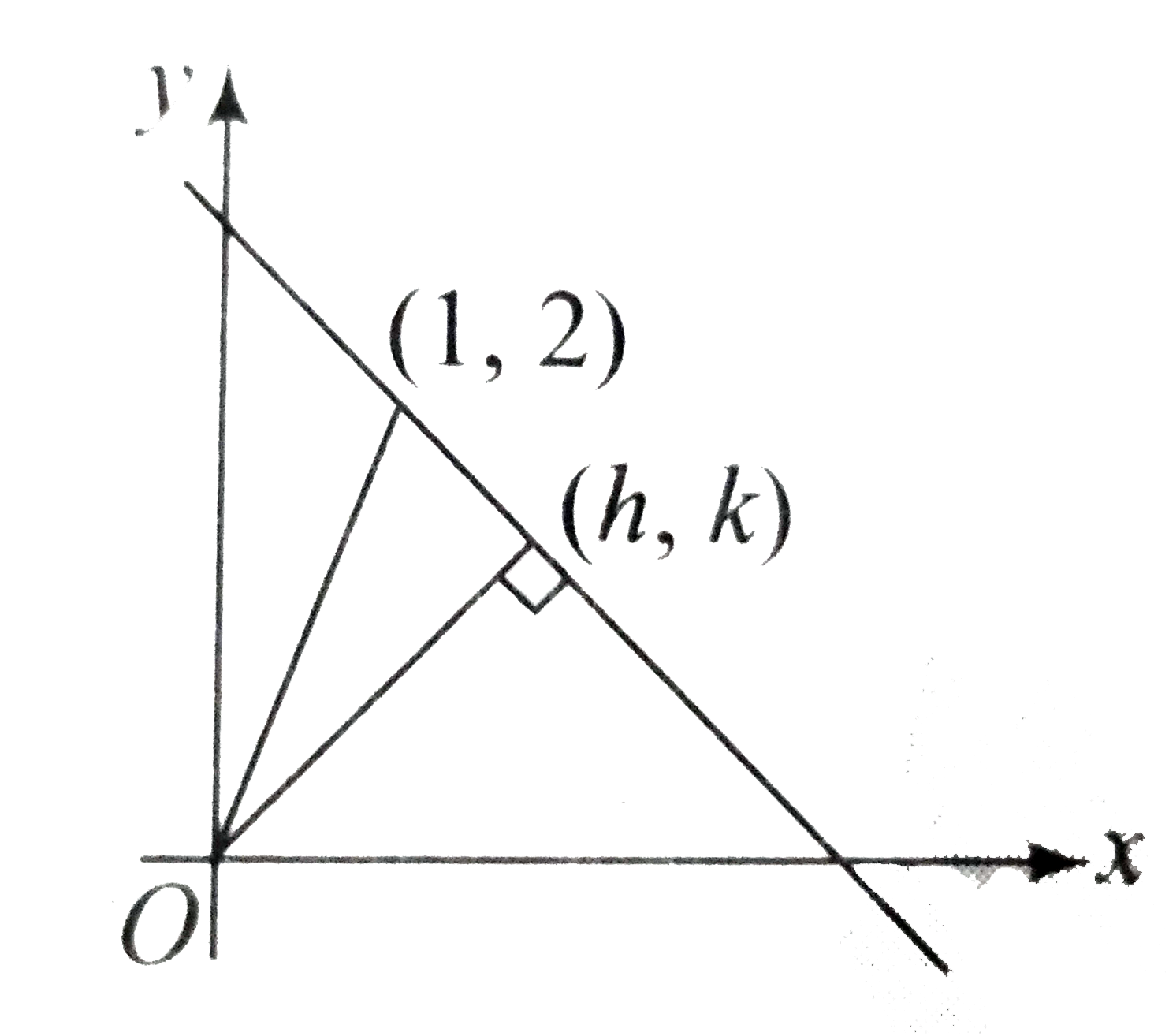
Now let (h,k) be the foot of perpendicular on each of the family.
∴kh.k−2h−1=−1
∴ Locus is x(x−1)+y(y−2)=0
or (2x−1)2+4(y−1)2=5
Topper's Solved these Questions
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Comprehension Type
3 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- STATISTICSBOOK - CENGAGECHAPTER - STATISTICSEXERCISE - JEE Previous Year
10 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year
4 Videos
Similar Questions
In a ΔABC,A=(2,3) and medians through B and C have equations x+y−1=0 and 2y−1=0
Equation of median through A is
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionIf the mean deviation of number 1,1+d, 1+2d,…., 1+100d from their mean is 255, then d is equal to
View Solutionabout to only mathematics
View SolutionThe locus of the foot of the perpendicular from the origin on each member of the family (4a+3)x-(a+1)y-(2a+1)=0
View SolutionConsider a family of lines (4a+3)x-(a+1)y-(2a+1)=0 where a in R a member of this family with positive gradient making an angle of 45with the line 3x-4y=2, is
View SolutionParagraph Consider a family of lines (4a+3)x-(a+1)y-(2a+1)=0 where a in R. The locus of the foot of the perpendicular from the origin on each member of this family,is
View SolutionThe locus of the foot of the perpendicular, from the origin to chords of the circle x^(2)+y^(2)-4x-6y-3=0 which subtend a right angle at the origin,is:
View SolutionThe foot of the perpendicular from A (1, 0, 0) to the line x−12=y+1−3=z+108 is
View SolutionThe equation of the locus of the foot of perpendicular drawn from (5, 6) on the family of lines (x−2)+λ(y−3)=0 (where λ∈R) is
View Solution" The locus of the vertices of the family of parabolas "y=ax2+2a2x+1" is "(a≠0)" a curve passing through the point "
View SolutionAandB are two variable points on xandy axes such that OA+OB=1/2. Then the locus of the foot of the perpendicular from the origin on the line AB is
View SolutionThe locus of the foot of the perpendicular drawn from the origin to any tangent to the hyperbola x236−y216=1 is
View SolutionThe locus of the foot of the perpendicular from the origin on each member of the family (4a+3)x−(a+1)y−(2a+1)=0 (a) (2x−1)2+4(y+1)2=5 (b) (2x−1)2+(y+1)2=5 (c) (2x+1)2+4(y−1)2=5 (d) (2x−1)2+4(y−1)2=5
View SolutionParabola y^2 = 4ax The locus of the poles of the chord of normal y^2(x + 2a) + 4a^3 = 0 is
View Solutionरेखाओ के निकाय (4 a + 3) x - (a + 1) y - (2 a + 1) = 0 पर विचार कीजिये, जहाँ a∈R है।
इस निकाय के प्रत्येक सदस्य पर (0,0) से डाले गये लम्ब के पाद का बिन्दुपथ होगा
View Solution
