Question

The acute angle between two straight lines passing through the point $M(-6,-8)$
and the points in which the line segment $2x+y+10=0$
enclosed between the co-ordinate axes is divided in the ratio 1:2:2 in
the direction from the point of its intersection with the x-axis to the point
of intersection with the y-axis is:
(a)$\frac{\pi }{3}$
(b) $\frac{\pi }{4}$
(c) $\frac{\pi }{6}$
(d) $\frac{\pi }{12}$

Options

A. `pi//3`
B. `pi//4`
C. `pi//6`
D. `pi//12`

Answer

B

Explanation

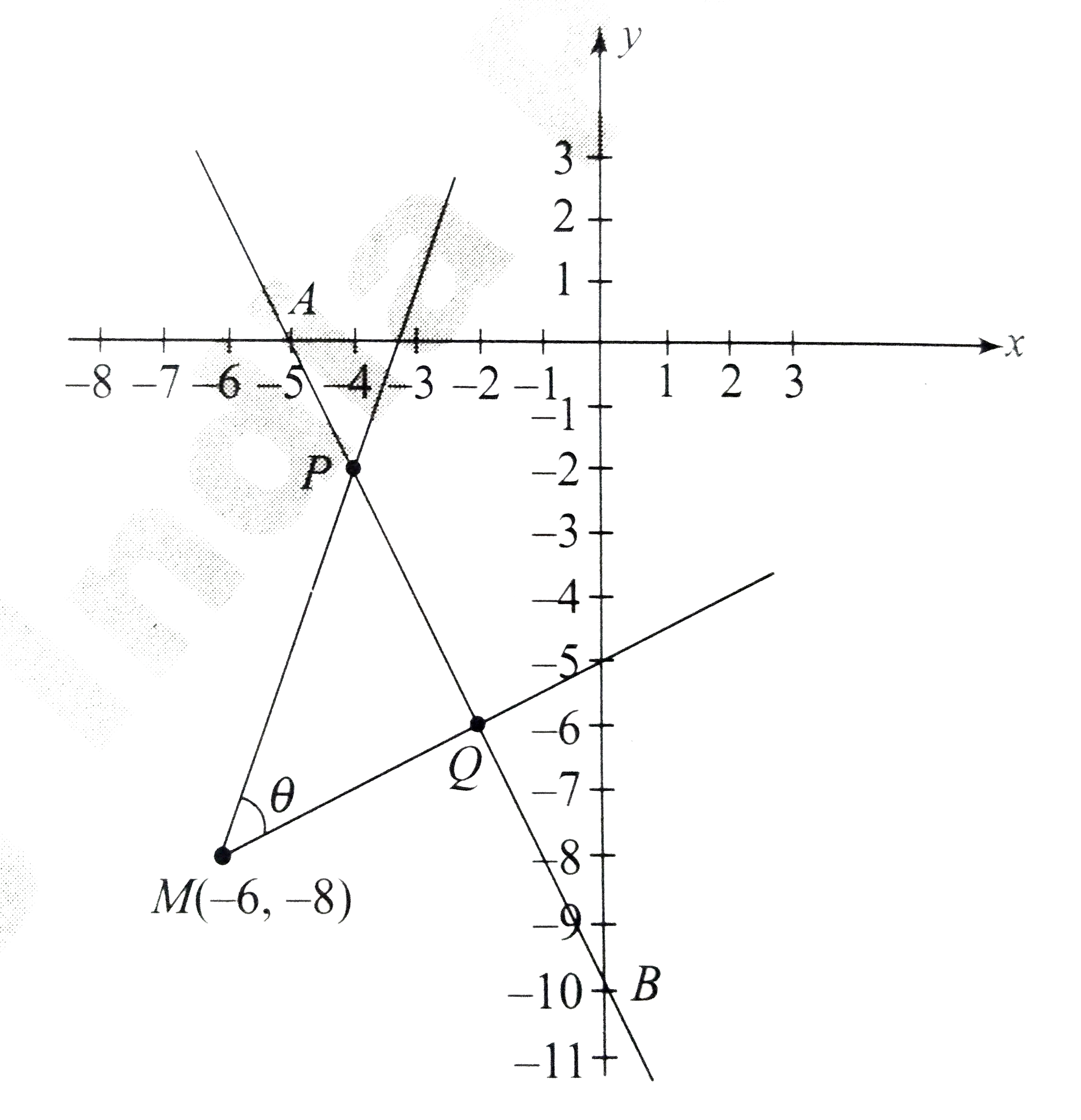
Le line `2x +y = 10 = 0` intersect axis at `A(-5,0)` and `B(0,-10)` Lines through point `M(-6,-8)` intersect AB at P and Q,
Slope of AB is `-2 = tan alpha`
Also `AB = sqrt(25+100) = 5sqrt(5)`
Given `AP: PQ: QB -= 1:2:2`
`:. AP = sqrt(5)` and `AQ = 3sqrt(5)`
Using parametric from of straight line AB, point P is `(-5-sqrt(4) cos alpha, 0 -sqrt(5) sin alpha)` or `P(-4,-2)`
Point Q is `(-5-3sqrt(5) cos alpha, 0-3 sqrt(5) sin alpha)` or `Q(-2,-6)`
`:.` Let slopes of PM and QM be `m_(1)` and `m_(2)`, respectively.
`:. m_(1) = 3` and `m_(2)=(1)/(2)`
Let `theta` be the acture angle between PM and QM.
`:. tan theta = |(m_(1)-m_(2))/(1+m_(2)m_(2))|`
`rArr tan theta = 1 rArr theta = (pi)/(4)`