The remainder when is divided by Solution in Tamil
The correct Answer is:D
Remainder is
Topper's Solved these Questions
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Multiple Correct Answer
4 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - JEE Previous Year
16 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
6 Videos
Similar Questions
Prove that ^nC2n0Cn−nC2n−21Cn+nC2n−42Cn≡2n.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionThe remainder left out when 82n(62)2n+1 is divided by 9 is (1) 0 (2) 2 (3) 7 (4) 8
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionFind the derivative of y=ln(cosx2).
View SolutionFind the remainder of 51^(51) when divided by 25.
View SolutionThe remainder when 2710+751 is divided by 10
View SolutionA number which when divided by 10 leaves a remainder of 9, when divided by 9 leaves a remainder of 8, and when divided by 8 leaves a remainder of 7 , is :
View SolutionThe remainder when 7128 is divided by 10 is
View SolutionThe remainder when 2710+751 is divided by 10 (a) 4 (b) 6 (c) 9 (d) 2
View SolutionFind the remainder when x51+51 is divided by x + 1.
View SolutionA number which when divided by 10 leaves a remainder of 9, when divided by 9 leaves a remainder of 8, and when divided by 8 leaves a remainder of 7 , is :
View SolutionThe remainder when
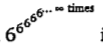 is divided by 10 is :
is divided by 10 is :
View SolutionFind the remainder when (2)51 is divided by 5.
View SolutionDivide each of the number by 10 and note down the remainder.Then,compare the remainder with the ones digit of the numer.(we do the first one for you ,when we divide 27 by 10 , we get a remainder of 7.)
.e.27=(2 xx 10)+7
27÷10=2,remainder 7. M
We see that the remainde is the same as the ones digit of 27.
View Solution
