Suppose ABCS (in order) is a quadrilateral inscribed in a circle. Which of the following is/are always true? secB=secD (b) cotA+cotC=0 cosecA=cosecC (d) tanB+tanD=0Solution in Tamil
secB=secB
cotA+cotC=0
cosecA=cosecC
tanB+tanD=0
The correct Answer is:B, C, D
Opposite angles of a cyclic quadrilateral are supplementary.
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Comprehension)
11 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Matrix)
3 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Single)
57 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type
1 Videos
Similar Questions
Let us consider the equation cos4xa+sin4xb=1a+b,x∈[0,π2],a,b>0
The value of sin2x in terms of a and b is
View Solution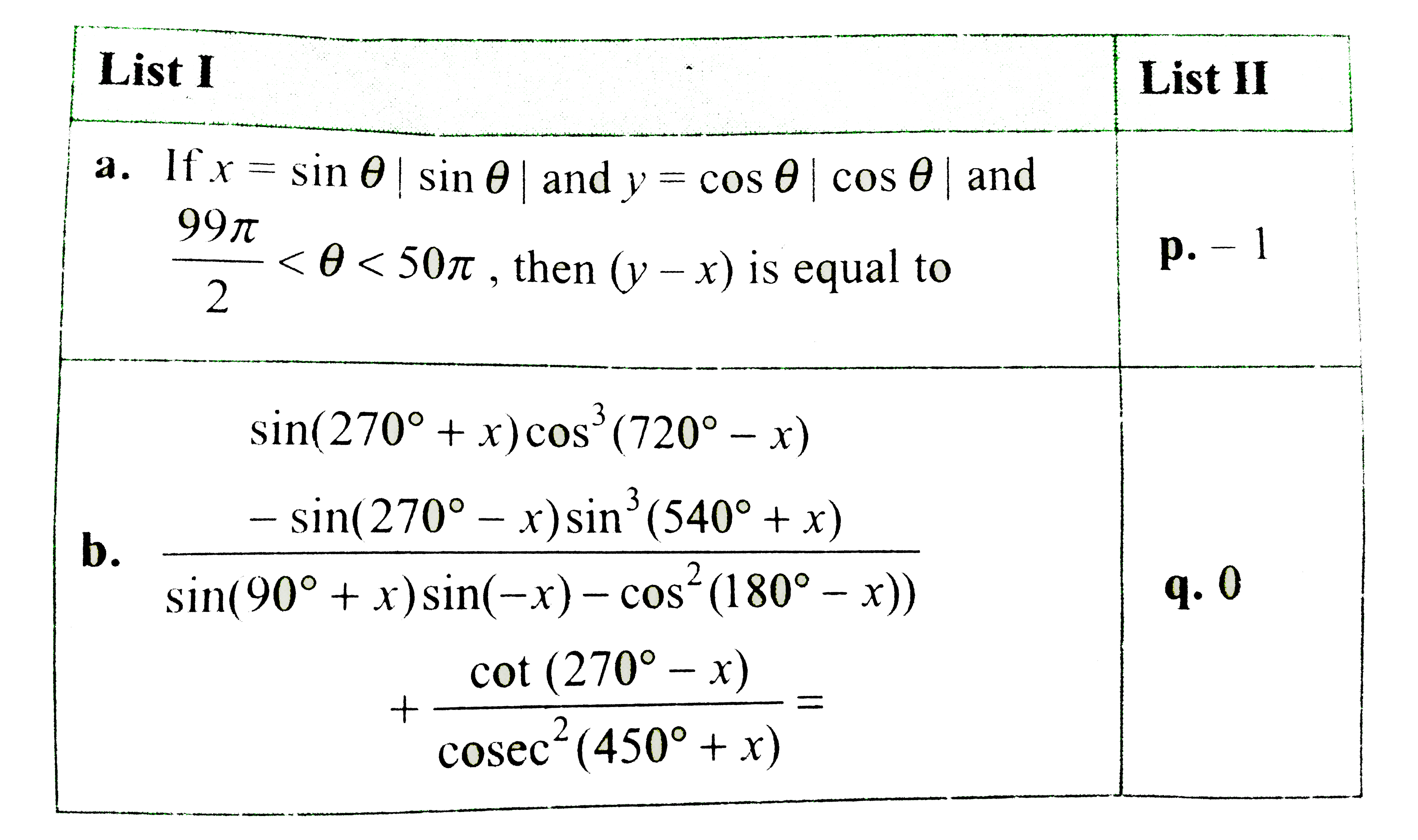
View SolutionIf 5tanθ=4, then 5sinθ−3cosθ5sinθ+2cosθ is equal to 0 (b) 1 (c) 16 (d) 6
View SolutionFind the derivative of y=tan−12x3
View SolutionRefer to the following diagram :

Column IColumn IIa.Collinear vectorsp.→ab.Coinitial vectorsq.→bc.Equal vectorsr.→cd.Unlike vectors (same initial point)s.→d
View SolutionSuppose ABCD (in order) is a quadrilateral inscribed in a circle. Which of the following is/are always true? secB=secD (b) cotA+cotC=0 cosecA=cosecC (d) tanB+tanD=0
View SolutionIf A,B,C,D be the angles of a quadrilateral, prove that : tanA+tanB+tanC+tanDcotA+cotB+cotC+cotD=tanAtanBtanCtanD
View SolutionIf A+B+C=π, prove that : (tanA+tanB+tanC)(cotA+cotB+cotC)=1+secAsecBsecC.
View SolutionIf A+B+C=π , prove that cotA+cotB+cotC−cosecA.cosecB.cosecC=cotA.cotB.cotC.
View SolutionSuppose ABCD (in order) is a quadrilateral inscribed in a circle. Which of the following is/are always true? secB=secD (b) cotA+cotC=0 cosecA=cosecC (d) tanB+tanD=0
View SolutionSuppose ABCS (in order) is a quadrilateral inscribed in a circle. Which of the following is/are always true? secB=secD (b) cotA+cotC=0 cosecA=cosecC (d) tanB+tanD=0
View SolutionIf A+B+C=π , prove that cotA+cotB+cotC−cosecA.cosecB.cosecC=cotA.cotB.cotC.
View SolutionProve the following identities: 1cosecA−cotA−1sinA=1sinA−1cosecA+cotA
View SolutionProve the following identities: cotA+cosecA−1cotA−cosecA+1=1+cosAsinA
View SolutionSuppose ABCD (in order) is a quadrilateral inscribed in a circle. Which of a following is/are always true ?
View SolutionIf A,B,C,D be the angles of a quadrilateral, prove that : tanA+tanB+tanC+tanDcotA+cotB+cotC+cotD=tanAtanBtanCtanD
View Solution
