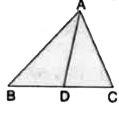
Given a right triangle ABC with $∠ A = 90^{0} .$ Let D be the mid-point of BC. If the inradii of the triangle $A B D$ and ACD are $r_{1} a n d r_{2}$ then find the range of $\frac{r_{1}}{r_{2}} .$ Solution in Tamil

Video Solution

Text Solution

Verified by Experts

In the figure, D is mid-point of BC. From the geometry, $A D = B D = C D = a / 2$
In $Δ A B D, r_{1} = \frac{Δ_{1}}{s_{1}}$
$\Rightarrow r_{1} = \frac{\frac{1}{2} (\frac{a}{2}) h}{\frac{\frac{a}{2} + \frac{a}{2} c}{2}}$
$\Rightarrow r_{1} = \frac{a h}{2 (a + c)}$

In $Δ A C D, r_{2} = \frac{Δ_{2}}{s_{2}}$
$\Rightarrow r_{2} = \frac{\frac{1}{2} (\frac{a}{2}) h}{\frac{\frac{a}{2} + \frac{a}{2} + b}{2}}$
$\Rightarrow r_{2} = \frac{a h}{2 (a + b)}$
$\Rightarrow \frac{r_{1}}{r_{2}} = \frac{a + b}{a + c}$
$= \frac{2 R sin A + 2 R sin B}{2 R sin A + 2 R sin C}$
$= \frac{1 + sin B}{1 + sin C} (as A = 90^{\circ})$
$= \frac{1 + sin B}{1 + cos B} (as C = 90^{\circ} - B)$
When B aproaches to $90^{\circ}, \frac{r_{1}}{r_{2}}$ approaches to 2
When B approaches to $0^{\circ}, \frac{r_{1}}{r_{2}}$ approaches to $\frac{1}{2}$
$∴ \frac{r_{1}}{r_{2}} \in (\frac{1}{2}, 2)$

|

Updated on:21/07/2023

Class 12 MATHS PROPERTIES AND SOLUTIONS OF TRIANGLE

Topper's Solved these Questions

Similar Questions

CENGAGE-PROPERTIES AND SOLUTIONS OF TRIANGLE-JEE Advanced Previous Year

Home
Ask Doubt
Profile