∫pxp+2q−1−qxq−1x2p+2q+2xp+q+1dx is equal to
(1) −xpxp+q+1+C
(2) xqxp+q+1+C
(3) −xqxp+q+1+C
(4) xpxp+q+1+C Solution in Tamil
−xpxp+q+1+C
xqxp+q+1+C
−xqxp+q+1+C
xpxp+q+1+C
The correct Answer is:C
∫pxp+2q−1−qxq−1(xp+q+1)2dx=∫pxp−1−qxq−1(xp+x−q)2dx (Dividing Nr and Dr by x2q)
=∫dtt2=−1t+C, where t=xp+x−q
=−1xp+x−q+C
=−xqxp+q+1+C
Topper's Solved these Questions
- INDEFINITE INTEGRATIONBOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercise (Multiple)
17 Videos
- INDEFINITE INTEGRATIONBOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercise (Comprehension)
17 Videos
- INDEFINITE INTEGRATIONBOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercise 7.9
15 Videos
- HYPERBOLABOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - JEE Advanced Previous Year
14 Videos
- INEQUALITIES AND MODULUSBOOK - CENGAGECHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer
21 Videos
Similar Questions
∫dx√2ex−1=
View Solutiony=f(x) is a polynomial function passing through point (0, 1) and which increases in the intervals (1,2)and(3,∞) and decreases in the intervals (∞,1)and(2,3).
If f(1)=−8, then the value of f(2) is
View SolutionEvaluate ∫sin2xdx
View SolutionLet P(6,3) be a point on the hyperbola x2a2−y2b2=1. If the normal at point P intersects the x-axis at (9, 0), then find the eccentricity of the hyperbola.
View SolutionIf f(x)=ax2+bx+c and f(−1)≥−4, f(1)≤0 and f(3)≥5, then the least value of a is
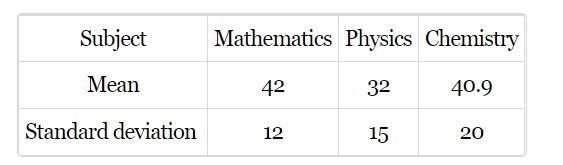
View SolutionThe mean and standard deviation of marks obtained by 50 students of a class in three subject, Mathematics, Physics and Chemistry are given below :
Which of the three subjects shows the highest variability in marks and which shows the lowest?
View SolutionIf a+c+e=0 and b+d=0, then ax^4+bx^3+cx^2+dx+e is exactly divisible by (1) x+1 (2) x-1 (3) Both (1) & (2) (4) None of these
View SolutionIf int (1+xtanx)^(-2) dx=1/(x+f(x))+c; then value of f(x) is (1) xtanx (2) cotx (3) tanx (4) tan^2x
View Solutionx=(sqrt(p^2+q^2)+sqrt(p^2-q^2))/(sqrt(p^2+q^2)-sqrt(p^2-q^2)) then q^2x^2-2p^2x+q^2=? (A) 3 (B) -1 (C) -2 (D) 0
View SolutionIf the lines ax+y+1=0 , x+by+1=0 and x+y+c=0 , ( a , b , c being distinct and different from 1 ) are concurrent, then 1/(1-a)+1/(1-b)+1/(1-c)= (A) 0 (B) 1 (C) 1/(a+b+c) (D) None of these
View SolutionWhich one of the following equations parametrically represents equation to a parametric profile ? (A) x=3cost ; y=4sint (B) x^2-2=-2cost ; y=4cos(t^2/2) (C) sqrt(x)=tant ; sqrt(y)=sect (D) x=sqrt(1-sint) ; y=sin(t/2)+cos(t/2)
View SolutionIf abx^2=(a-b)^2(x+1) , then the value of 1+4/x+4/x^2 is: a. (a+b)/(a-b) b. (a+b)^2/(a-b)^2 c. (a+b)/(a-b)^2 d. 1
View SolutionIn an AP, S_p=q , S_q=p . Then S_(p+q) is equal to: a. 0 b. -(p+q) c. (p+q) d. pq
View SolutionIf alpha , beta gamma are the roots of the equation x^3+px^2+qx+r=0 , then (1-alpha^2)(1-beta^2)(1-gamma^2) is equal to (a) (1+q)^2-(p-r)^2 (b) (1+q)^2+(p+r)^2 (c) (1-q)^2+(p-r)^2 (d) none of these
View SolutionIf m and x are two real numbers where m∈I, then e2micot−1x(x⋅i+1x⋅i−1)m
(A) cosx+isinx (B) m2 (C) 1 (D) m+12
View Solution