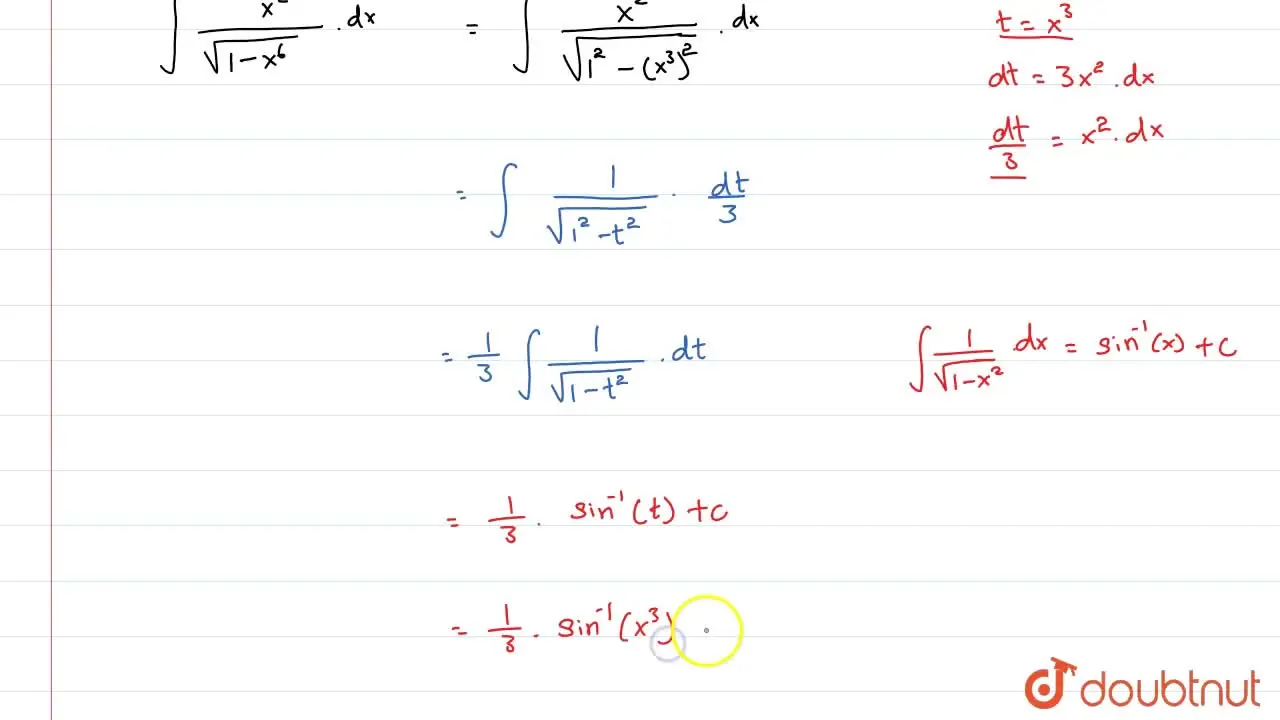Evaluate: ∫x2√1−x6dxSolution in Tamil
The correct Answer is:13sin−1(x3)+C
I=∫x2√1−x6dx=∫x2√12−(x3)2dx
Let x3dx=dt
∴I=13∫dt√1−t2=13sin−1(t)+C=13sin−1(x3)+C
Related Playlists
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercise 7.710videos
INDEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercise 7.87videos
INDEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercise 7.59videos
INDEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - JEE Advanced Previous Year14videos
HYPERBOLA
- BOOK - CENGAGECHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer21videos
INEQUALITIES AND MODULUS
Similar Questions
Evaluate ∫13+sin2xdx.
03:03View SolutionEvaluate: ∫1(x2−4)√x+1dx
02:17View SolutionEvaluate ∫dx1−x−x2
04:47View SolutionLet P(6,3) be a point on the hyperbola x2a2−y2b2=1. If the normal at point P intersects the x-axis at (9, 0), then find the eccentricity of the hyperbola.
02:56View SolutionIf f(x)=ax2+bx+c and f(−1)≥−4, f(1)≤0 and f(3)≥5, then the least value of a is
02:50View SolutionEvaluate: ∫x2√a6−x6dx
02:38View SolutionEvaluate: ∫x2√1−x6dx
08:24View SolutionEvaluate: (i) ∫1√x(1+1x) dx (ii) ∫x6+1x2+1 dx
09:11View SolutionEvaluate: (i) ∫ex√4−e2x dx (ii) ∫x2√1−x6 dx
02:38View SolutionEvaluate: ∫x2 √a6−x6 dx
06:46View SolutionEvaluate: ∫dx(x2+5x+6)√x+1
01:20View SolutionEvaluate :
(i) ∫dx1+√x (ii) ∫x+√x+1x+2dx03:37View Solutionनिम्नलिखित का मान ज्ञात कीजिए -
(a) ∫dx√(2−x)2+1 (b) ∫x2dx√a6+x6
(c) ∫exdx√4+e2x (d) ∫x−1√x2+1dx02:45View SolutionEvaluate :
∫1√x+1+√x+2dx03:52View SolutionEvaluate : ∫x+2√x2+5x+6dx.
02:55View SolutionEvaluate: ∫x2√1−x6dx
02:00View Solution