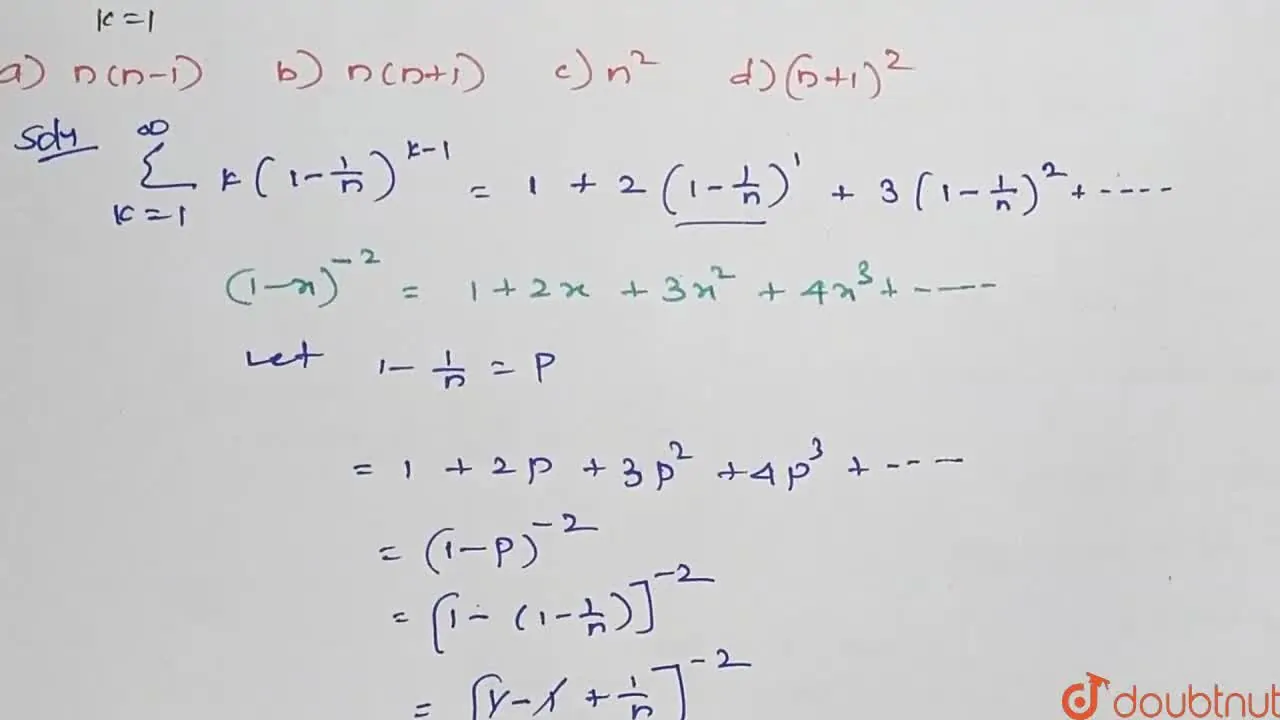∞∑k=1k(1−1n)k−1= n(n−1) b. n(n+1) c. n2 d. (n+1)2Solution in Tamil
n(n−1)
n(n+1)
n2
(n+1)2
The correct Answer is:C
∞∑k=1k(1−1n)k=1
=1−2(1−1n)1+3(1+1n)2+…..
=1+2r+3t2+…
=(1−t)−2
=[1−(1−1n)]−2=(1n)−2=n2
Related Playlists
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Exercise (Multiple)27videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Exercise (Comprehension)20videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Exercise 8.810videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE6videos
CIRCLE
Similar Questions
The value of x in the expression (x+x(log)10)5 if third term in the expansion is 10,00,000 is/are a. 10 b. 100 c. 10−5/2 d. 10−3/2
02:18View SolutionThe sixth term in the expansion of (√2log(10−3x)+(2(x−2)log3)15)m is equal to 21, if it is known that the binomial coefficient of the 2nd 3rd and 4th terms in the expansion represent, respectively, the first, third and fifth terms of an A.P. (the symbol log stands for logarithm to the base 10) The value of m is
04:10View SolutionIf the third term in the expansion of (1+x)mis−18x2, then find the value of m.
10:33View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
02:11View SolutionFind the derivative of y=ln(cosx2).
06:59View Solution∞∑k=1k(1−1n)k−1= a.n(n−1) b. n(n+1) c. n2 d. (n+1)2
03:29View Solutionprove that sum_(k=1)^(n)k2^(-k)=2[1-2^(-n)-n*2^(-(n+1)))
05:41View SolutionS_(n)=sum_(k=1)^(n)(k^(2)+n^(2))/(n^(3)) and T_(n)=sum_(k=0)^(n-1)(k^(2)+n^(2))/(n^(3)),n in N then
07:46View SolutionIf n∈N,n∑k=1sin−1(xk)=nπ2t h e nn∑k=1xk
09:21View SolutionIf sum_(n=1)^(5)(1)/(n(n+1)(n+2)(n+3))=(k)/(3), then k is equal to :-
View SolutionLet a_(n)=sum_(k=1)^(n)(1)/(k(n+1-k)), then for n>=2
02:40View SolutionIf sum_(k=1)^n(sum_(m=1)^k m^2)=a n^4+b n^3+c n^2+dn+e then -
05:36View SolutionLet Sn=n∑k=1nn2+nk+k2andTn=n−1∑k=0nn2+nk+k2 for n=1,2,3..., then
03:20View Solutionn∑k=1k(1+1n)k−1 =
03:03View Solution∞∑n=11k!(k∑n=12n−1)=
01:43View Solution∞∑k=1k(1+1n)k−1=
02:29View Solution