For a given point A(0,0), ABCD is a rhombus of side 10 units where slope of AB is 43and slope of AD is 34. The sum of abscissa and ordinate of point C (where C lies in first quadrant) is Solution in Tamil
The correct Answer is:B(6,8),C(14,14),D(8,6)
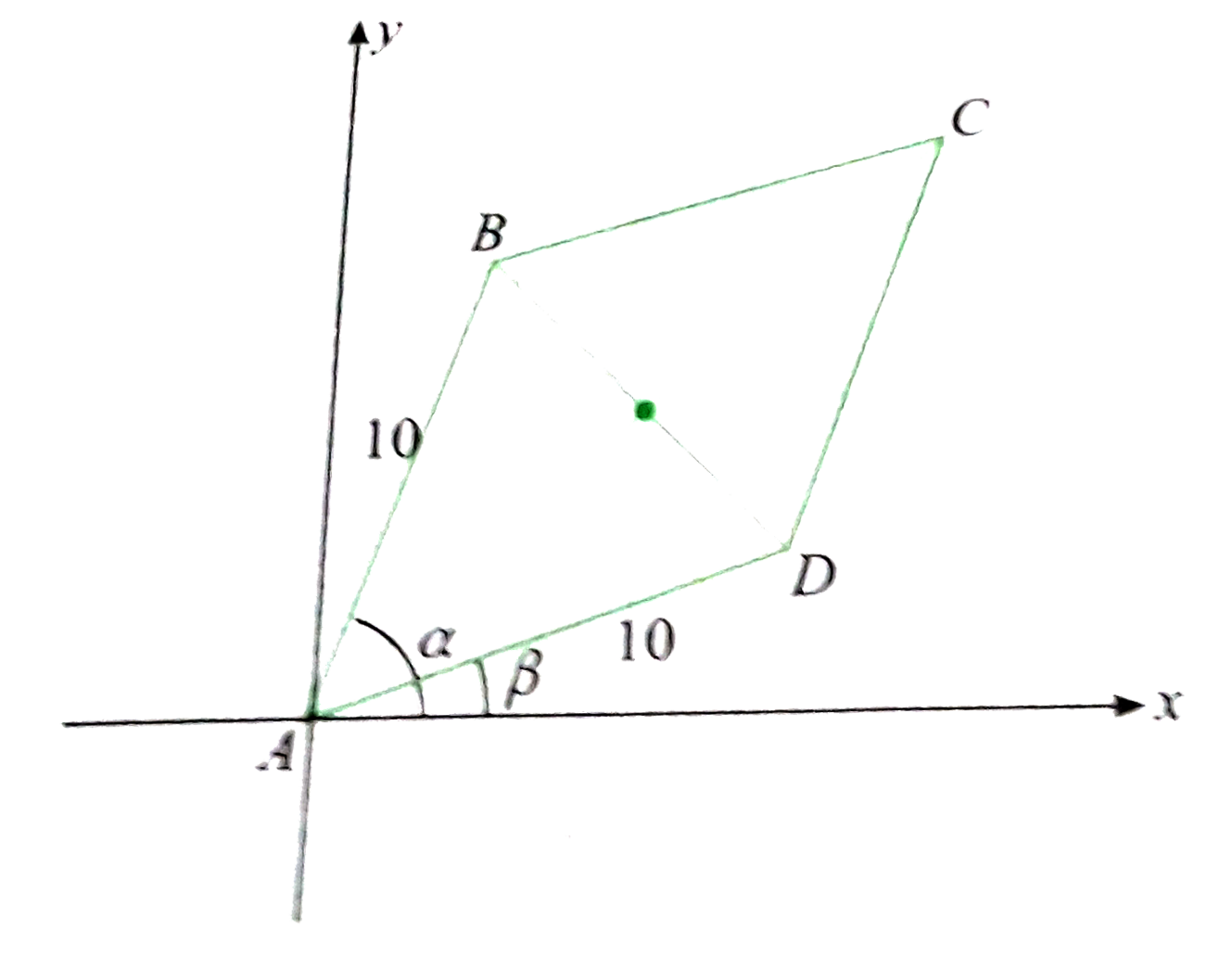
In the figure,tanα=43
∴ Coordinates of point B
≡(10cosα,10sinα)
≡(10×35,10×45)≡(6,8)
Also, tanβ=34
∴ coordinates of Point D
≡(10cosβ,10sinβ)
≡(10×45,10×35)≡(8,6)
Diagonals of rhombus bisect. So, midpoint of BD is (7,7) which is midpoint of AC. therefore, coordinates of C are (14,14).
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.5
5 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.6
9 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.3
10 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Convert the following polar coordinates to its equivalent Cartesian coordinates.
(i) (2,π)
(ii) (√3,π/6)
View SolutionFind the locus of a point whose distance from (a, 0) is equal to its distance from the y-axis.
View SolutionIf point P(3,2) divides the line segment AB internally in the ratio of 3:2 and point Q(−2,3) divides AB externally in the ratio 4:3 then find the coordinates of points A and B.
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionPoint A and B are in the first quadrant,point O is the origin. If the slope of OA is 1,slope of OB is 7 and OA=OB,Then slope of AB is: a. -1/5 b. -1/4 c. -1/3 d. -1/2
View SolutionThe slope of the tangent to the curve y=√4−x2 at the point where the ordinate and the abscissa are equal is −1 (b) 1 (c) 0 (d) none of these
View SolutionPoint A and B are in the first quadrant; point O is the origin. If the slope of OA is 1, the slope of OB is 7, and OA=OB, then the slope of AB is −15 (b) −14 (c) −13 (d) −12
View SolutionFor a given point A(0,0),ABCD is a rhombus of side 10 units where slope of AB is (4)/(3) and slope of AD is (3)/(4). The sum of abscissa and ordinate of point C (where C lies in first quadrant) is
View SolutionA straight line has slope (3)/(4) and it passes through the point A(-2,-5). Find the co- ordinates of a point B on this line where bar(AB)=10 unit.
View SolutionFind the equation of the curve passing through the point (0,0) and whose slope of the normal at a point (x, y) is equal to the sum of the ordinate and the product of the abscissa and ordinate of that point.
View SolutionThe slope of the tangent at any arbitrary point of a curve is twice the product of the abscissa and square of the ordinate of the point. Then, the equation of the curve is (where c is an arbitrary constant)
View SolutionThe slope of normal at any point P of a curve (lying in the first quadrant) is reciprocal of twice the product of the abscissa and the ordinate of point P. Then, the equation of the curve is (where, c is an arbitrary constant)
View SolutionThe slope of the tangent to the curve y=√4−x2 at the point where the ordinate and the abscissa are equal is (a)−1 (b) 1 (c) 0 (d) none of these
View SolutionFor a given point A(0,0), ABCD is a rhombus of side 10 units where slope of AB is 43and slope of AD is 34. The sum of abscissa and ordinate of point C (where C lies in first quadrant) is
View Solution
