Find tan−1x√a2−x2 in terms of sin−1 where x∈(0,a).Solution in Tamil
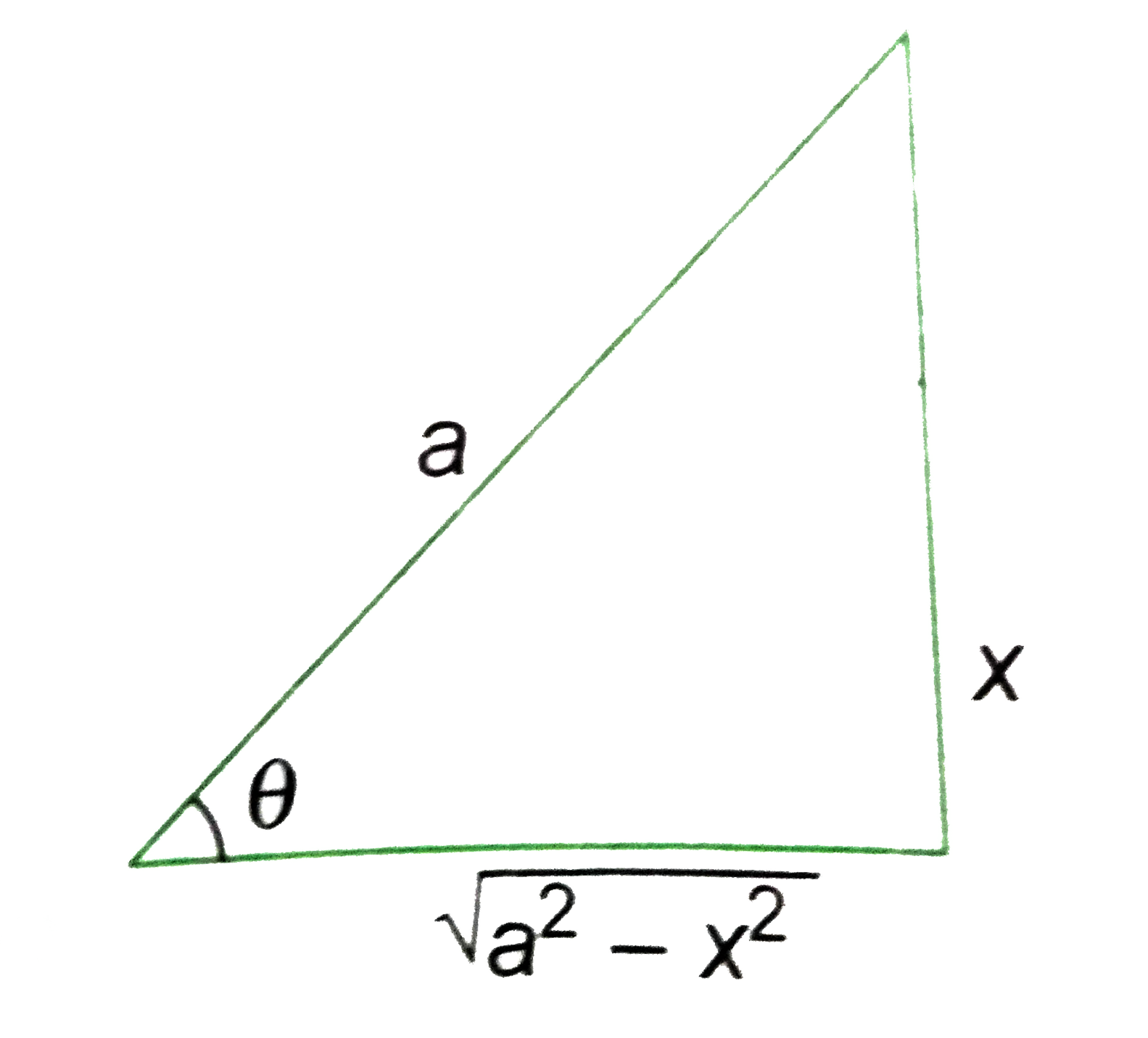
We have tan−1(x)√a2−x2=θ
From the triangle,
tan−1(x)√a2−x2=sin−1(x)a
Topper's Solved these Questions
Similar Questions
Find the values of λ such that x,y,z≠(0,0,0)and(ˆi+ˆj+3ˆk)x+(3ˆi−3ˆj+ˆk)y+(−4ˆi+5ˆj)z=λ(xˆi+yˆj+zˆk),whereˆi,ˆjandˆk are unit vector along coordinate axes.
View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
View SolutionFind tan−1x√a2−x2 in terms of sin−1 where x∈(0,a).
View SolutionF i n ddydxify=tan−1(√1+x2−1x), where x≠0
View Solutiony=tan−1(√1+x2+√1−x2√1+x2−√1−x2),where −1<x<1,x≠0
View Solutionif x greater than equal to 0 and less than equal to 1/2 then find the value of tan[sin^(-1){(x)/(sqrt(2))+sqrt((1-x^(2))/(2))}-sin^(-1)x]
View SolutionFind tan−1.x√a2−x2 in terms of sin−1, where x∈(0,a)
View SolutionIf y=tan−1[√1+sinx−√1−sinx√1+sinx+√1−sinx] where 0<x<π2 find dydx
View SolutionFind tan−1x√a2−x2 in terms of sin−1 where x∈(0,a).
View SolutionEvaluate: ∫etan−1x(1+x2)[(sec−1√1+x2+cos−1(1−x21+x2)]dx,(x>0).
View SolutionFind tan−1.x√a2−x2 in terms of sin−1, where x∈(0,a)
View SolutionIf y=sin−1[x√1−x−√x√1−x2) and 0<x<1, then find dydx.
View SolutionFinddydxify=tan−1(√1+x2−1x), where x≠0
View SolutionEvaluate: ∫etan^−1(x)(1+x2)[(sec−1√1+x2)2+cos−1(1−x21+x2)]dx(x>0).
View SolutionEvaluate: ∫etan^((−1)x)(1+x2)[((sec−1√1+x2)2+cos−1(1−x21+x2)]dx(x>0).
View SolutionFind tan−1x√a2−x2 in terms of sin−1 where x∈(0,a).
View Solution