A triangle is formed by the lines whose equations are AB: x+y-5=0, BC: x+7y-7=0 and CA: 7x+y+14=0.
ThenSolution in Tamil
angle at A is acute
angle at C is acute
internal angle bisector at angle B is 3x+6y-16=0
external angle bisector at angle C is 8x+8y+7 = 0
The correct Answer is:A, C, D
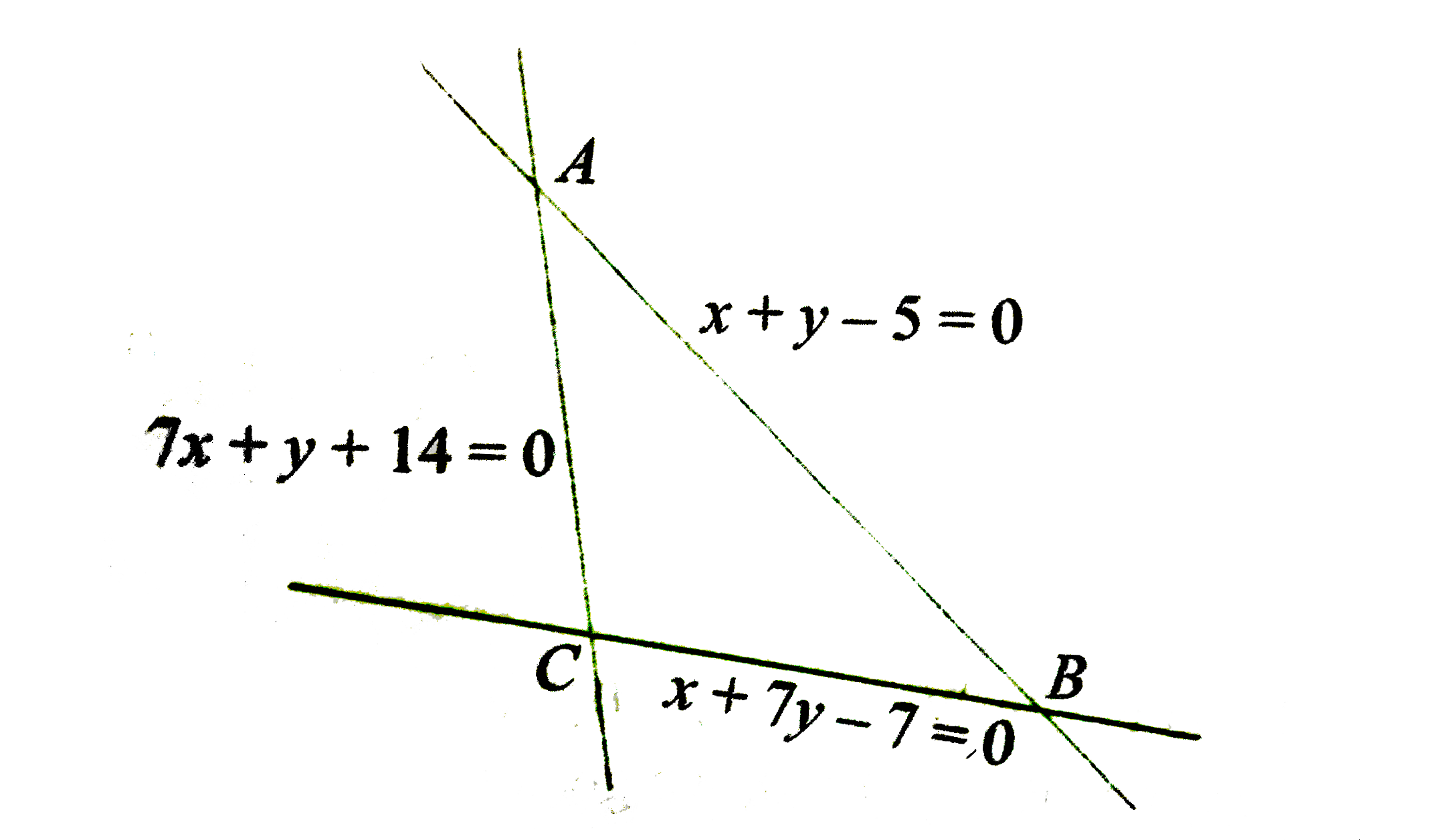
The slopes of the line AB, BC and CA are -1, −17 and -7, respectively,
Let m1=−17,m2=−1,m3=−7.
∴m1>m2>m3
So, tangent fo internal angles of the triangle are
tanA=34,tanB=34 and tanC=−247
So, interior angles A and B are acute and interior angle C is abtuse.
∴ Internal bisector of B ≡ Acute angle bisector at B
≡ Acute angle bisector of lines AB and BC
≡3x+6y−16=0
External bisector of C ≡ Acute bisector of C
≡ Acute angle bisector of lines AC and BC
≡8x+8y+7=0
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Comprehension)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Matrix)
Explore 8 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Single)
Explore 82 Videos
- STRAIGHT LINEBook:CENGAGEChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:JEE Advanced Previous Year
Explore 9 Videos
Similar Questions
Let L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b ∈R, which is the farthest from the point (2, 2).
Area enclosed by the line L and the coordinate axes is
View SolutionConsider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:

View SolutionFind the equations of the diagonals of the square formed by the lines x=o,y=0,x=1andy=1.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionThe orthocentre of the triangle formed by the lines x-7y+6=0,2x-5y-6=0 and 7x+y-8=0 is
View SolutionFind the area of the triangle formed by the straight line whose equations are 2y+x-5=0,y+2x-7=0 and x-y+1=0
View SolutionA triangle is formed by the lines whose equations are AB: x+y-5=0, BC: x+7y-7=0 and CA: 7x+y+14=0.
Then
View SolutionLines y=−7x+5 and x−7y+4=0 are perpendicular.
View SolutionA triangle is formed by the lines whose equations are AB: x+y-5=0, BC: x+7y-7=0 and CA: 7x+y+14=0.
Then
View SolutionA triangle is formed by three lines AB: x + y-5 = 0, BC: x + 7y-7 = 0 and CA: 7x + y-14 = 0. Find the inner bisector of angle B and the outer bisector of angle C. Determine the nature of the interior angle at point A and find the equation of the bisector.
View SolutionFind the orthocentre of the triangle formed by 4x−7y+10=0,x+y−5=0,7x+4y−15=0.
View SolutionThe orthocentre of the triangle whose sides are given by 4x−7y+10=0,x+y−5=0 and 7x+4y−15=0
View Solutionरेखाओ 4 x - 7y + 10 = 0, x + y = 5 तथा 7x + 4y = 15 द्वारा बनाए गए त्रिभुज का लम्बकेन्द्र है
View Solutionत्रिभुज ABC की भुजाओ BC, CA तथा AB के समीकरण क्रमशः x - 2y + 5 = 0, x + y + 2 = 0 तथा 8 x - y - 20 = 0 है।
ΔABC का क्षेत्रफल बराबर है
View Solutionत्रिभुज ABC की भुजाओ BC, CA तथा AB के समीकरण क्रमशः x - 2y + 5 = 0, x + y + 2 = 0 तथा 8 x - y - 20 = 0 है।
ΔABC का लम्बकेन्द्र है
View Solution
