ABC is an isosceles triangle inscribed in a circle of radius $r .$ If $A B = A C$ and $h$ is the altitude from $A$ to $B C,$ then triangle $A B C$ has perimeter $P = 2 (\sqrt{2 h r - h^{2}} + \sqrt{2 h r})$ and area A= ____________ and also ${(lim)}_{h \to 0} \frac{A}{P^{3}} =_{_}__{_}_$ Solution in Tamil

Video Solution

Text Solution

Verified by Experts

In $Δ A B C, A B = A C, A D ⊥ B C (D is midpoint of B C)$

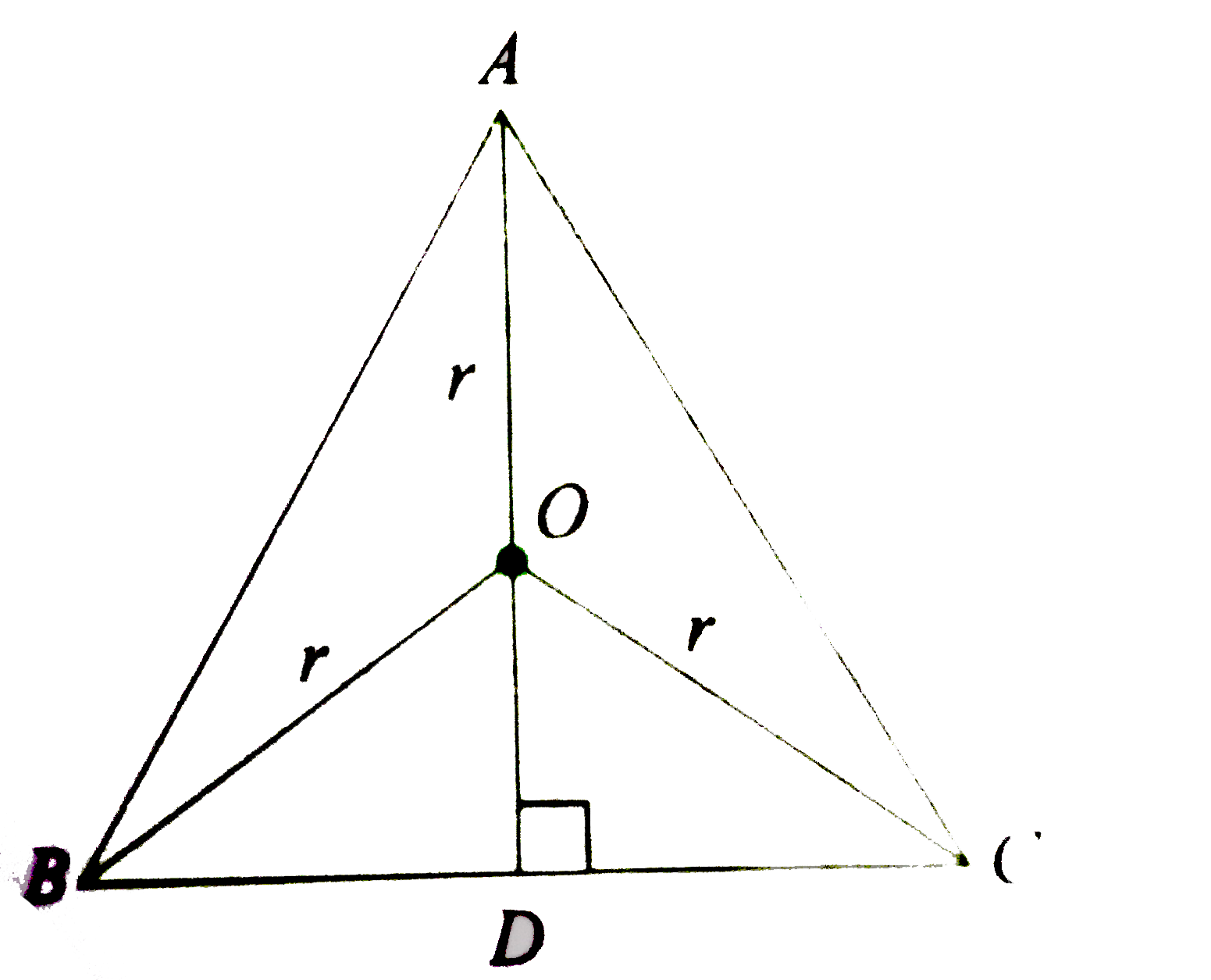
Let r= radius of circumcircle
$∴ O A = O B = O C = r$
Now $B D = \sqrt{B O^{2} - O D^{2}} = \sqrt{r^{2} - {(h - r)}^{2}} = \sqrt{2 r h - h^{2}}$
$∴ B C = 2 \sqrt{2 r h - h^{2}}$
Also $A B^{2} = B D^{2} + A D^{2} = 2 h r - h^{2} + h^{2} = 2 h r$ .
$∴ A B = A C = \sqrt{2 h r}$
$∴ Perimeter, P = 2 \sqrt{2 r h - h^{2}} + 2 \sqrt{2 h r}$
$∴ Area of Δ A B C = \frac{1}{2} \times B C \times A D = h \sqrt{2 r h - h^{2}}$
So, $lim h \to 0 \frac{A}{P^{3}} = \frac{h \sqrt{2 r h - h^{2}}}{8 {(\sqrt{2 r h - h^{2}} + \sqrt{2 h r})}^{3}}$
$= lim h \to 0 \frac{h^{3 / 2} \sqrt{2 r - h}}{8 h^{3 / 2 {(\sqrt{2 r - h} + \sqrt{2 r})}^{3}}}$
$= lim h \to 0 \frac{\sqrt{2 r - h}}{8 {[\sqrt{2 r - h} + \sqrt{2 r}]}^{3}}$
$= \frac{\sqrt{2 r}}{8 {(\sqrt{2 r} + \sqrt{2 r})}^{3}} = \frac{1}{128 r}$

Updated on:21/07/2023

|

Class 12 MATHS LIMITS AND DERIVATIVES

Topper's Solved these Questions

Similar Questions

CENGAGE-LIMITS-Question Bank

Home
Ask Doubt
Profile