The angle of elevation of the top of a tower a point A due south of it is 30∘ and from a point B due west of it is 45∘ .If the height of the tower is 100 meters ,then find the distance AB.Solution in Tamil
400
50
100
200
The correct Answer is:D
In the following figure OP is the tower .
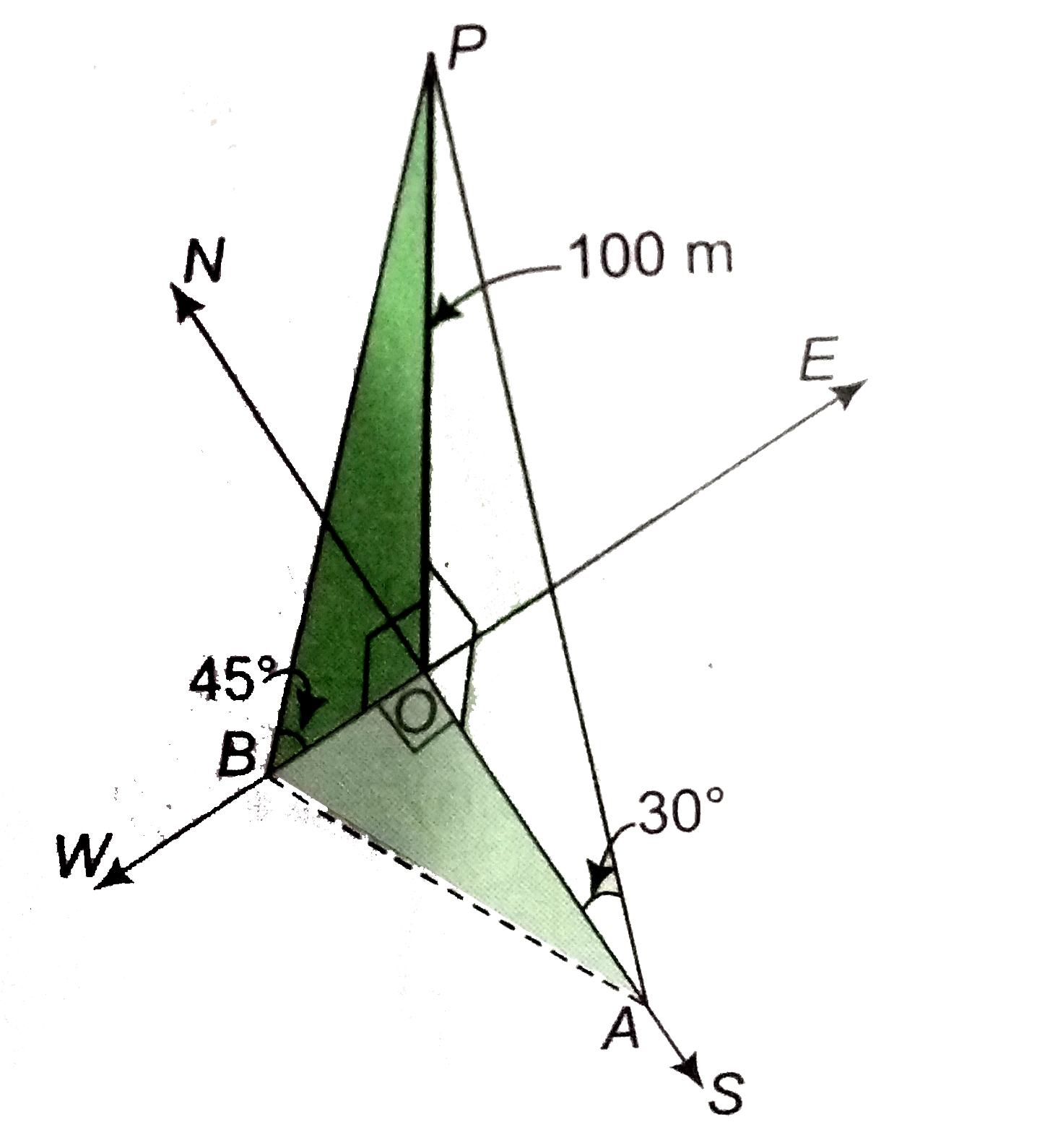
Op= 100 m
In right angled triangle :POA ,
tan30∘=100OA
∴OA=100cot30∘=100√3
In right angled triangle POB,
tan45∘=100OB
∴OB=100cot45∘=100
In right angled triangle AOB, using Pythagoras theorem ,we get
AB2=OA2+OB2
=3×1002+1002
=4×1002
∴AB=2×100=200m
Topper's Solved these Questions
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - Exercise
18 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- HYPERBOLABOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - JEE Advanced Previous Year
14 Videos
Similar Questions
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30o with horizontal, then the length of the wire is (a) 12 m (b) 10 m (c) 8 m (d) 6 m
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionLet P(6,3) be a point on the hyperbola x2a2−y2b2=1. If the normal at point P intersects the x-axis at (9, 0), then find the eccentricity of the hyperbola.
View SolutionFrom a point A due North of a tower,the angle of elevation of the top of the tower is 30^(@). From a point B due South,the elevation is 45^(@). If AB=100 metres,find the height of the tower
View SolutionAngle of elevation of top of a tower from a point 'A' due E30∘N of tower on the ground is 45∘. While angle of elevation of top of tower from a point 'B' due N60∘W of tower is 30∘ where AB=50 m, then height of tower is
View Solutionएक मीनार के पाद से 40 मीटर दुरी पर स्तिथित किसी बिनु से मीनार के शिखर का उनयन कोण 30∘ है मीनार की उचाई ज्ञात कीजिएः
View SolutionThe angular elevation of a tower OP at a point A due south of it is 60∘ and at a point B due west of A, the elevation is 30∘. If AB=3m, the height of the tower is
View SolutionThe angle of elevation of the top of a vertical tower from a point A due east of it is 45∘. The angle of elevation of the top of the same tower from a point B due south of A is 30∘. If the distance between A and B is 54√2 m then the height of the tower (in metres), is
View SolutionThe angular elevations of a tower CD at a place A due south of it is 60∘ , and at a place B due west of A, the elevation is 30∘ . If AB=300m, what is the height, in meters, of the tower?
View SolutionThe angle of elevation of the top of a tower at a point A due south of the tower is α and at β due east of the tower is β. If AB=d, then height of the tower is
View Solutionकिसी बिंदु से 100 मीटर की दूरी पर स्थित किसी मीनार के शीर्ष का उन्नयन कोण 45∘ है, तब मीनार की ऊँचाई होगी-
View SolutionThe elevation of a tower at a station A due north of it is 45∘ and at a station B due west of A is 30∘.
If AB=40 m, find the height of the tower:
View SolutionAngle of elevation of the top of the tower from station A to the west of a tower 45^(@) is. Station B, located 10 meters from A, to the south of the east of the tower 45^(@) Angle of elevation of the top of the tower from 30^(@) Is the height of the tower
View Solutionएक मीनार के दक्षिण की ओर बिन्दु A पर मीनार का उन्नयन कोण 45∘ तथा उत्तर की ओर स्थित बिन्दु B पर मीनार का उन्नयन कोण 45∘ हैं यदि मीनार की ऊँचाई 100 मीटर हो तो AB=
View SolutionThe angle of elevation of the top of the top of a vertical tower from a point A, due east of it is 45∘. The angle of elevation of the top of the same tower from a point B, due south of A is 30∘. If the distance between A and B is 54√2m, then the height of the tower (in meters), is
View Solution
