Question

Evaluate : $\underset{x\to 0}{lim}\frac{\sin x}{x}$

Explanation

Let us first draw the graphs of y = x and y = sin x.
For y = x, y' = 1, i.e. the slope of line is 1 for all real x.
For y = sin x, y' = cos x.
Thus, both y = x and y = sin x have slope '1' at x = 0, hence the graphs touch each other at x = 0.
Moving from '0' to `'pi//2'`, the values of cos x decrease from '1' to '0'.
Thus, the graph of y = sin x lies below the graph of y = x.
The graphs of y = x and y = sin x are plotted as follows.

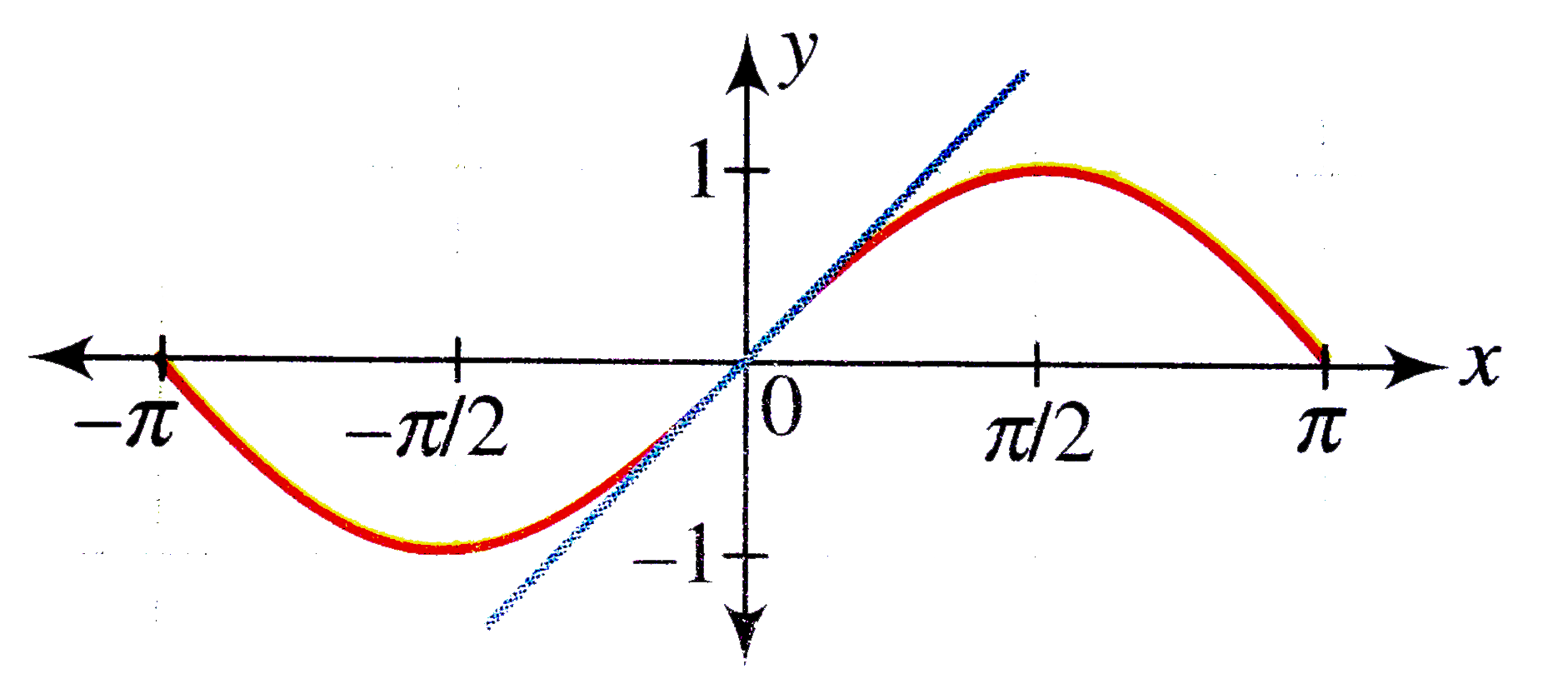
From the graph, when `x to 0^(+)`, as the graph of y = x is above the graph of y = sin x,
`sin x lt x rArr (sin x)/(x) lt 1 rArr[underset(x to 0^(+))lim (sin x)/(x)] = 0`
When `x to 0^(-)`, as the graph of y = x is below the graph of y = sin x,
`sin x gt x rArr (sin x)/(x) lt 1` (as x is negative) `rArr[underset(x to 0^(-))lim (sin x)/(x)] = 0`
Thus, `[underset(x to 0)lim (sin x)/(x)] = 0`