Question

Out of 100 students, 15 passed in English, 12 passed in Mathmatics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science , 4 in English and Science, 4 in all the three. Find how many passed
(i) in English and Mathematics but not in Science.
(ii) in Mathematics and Science but not in English.
(iii) in Mathematics only.
(iv) in more than one subject only.

Answer

(a) 2 (b) 3 ( c) 3 (d) 9

Explanation

Let M be the set of students who passed in Mathematics , E be the set of students who passed in English and S be the set of students who passed in Science

Given n( U)= 100
n( E) = 15 , n( M ) = 12 , n(s) = 8
` n( E cap M ) = 6 , n( M cap S) = 7 `
`n( E cap S ) = 4 and n( E cap M cap S ) = 4 `
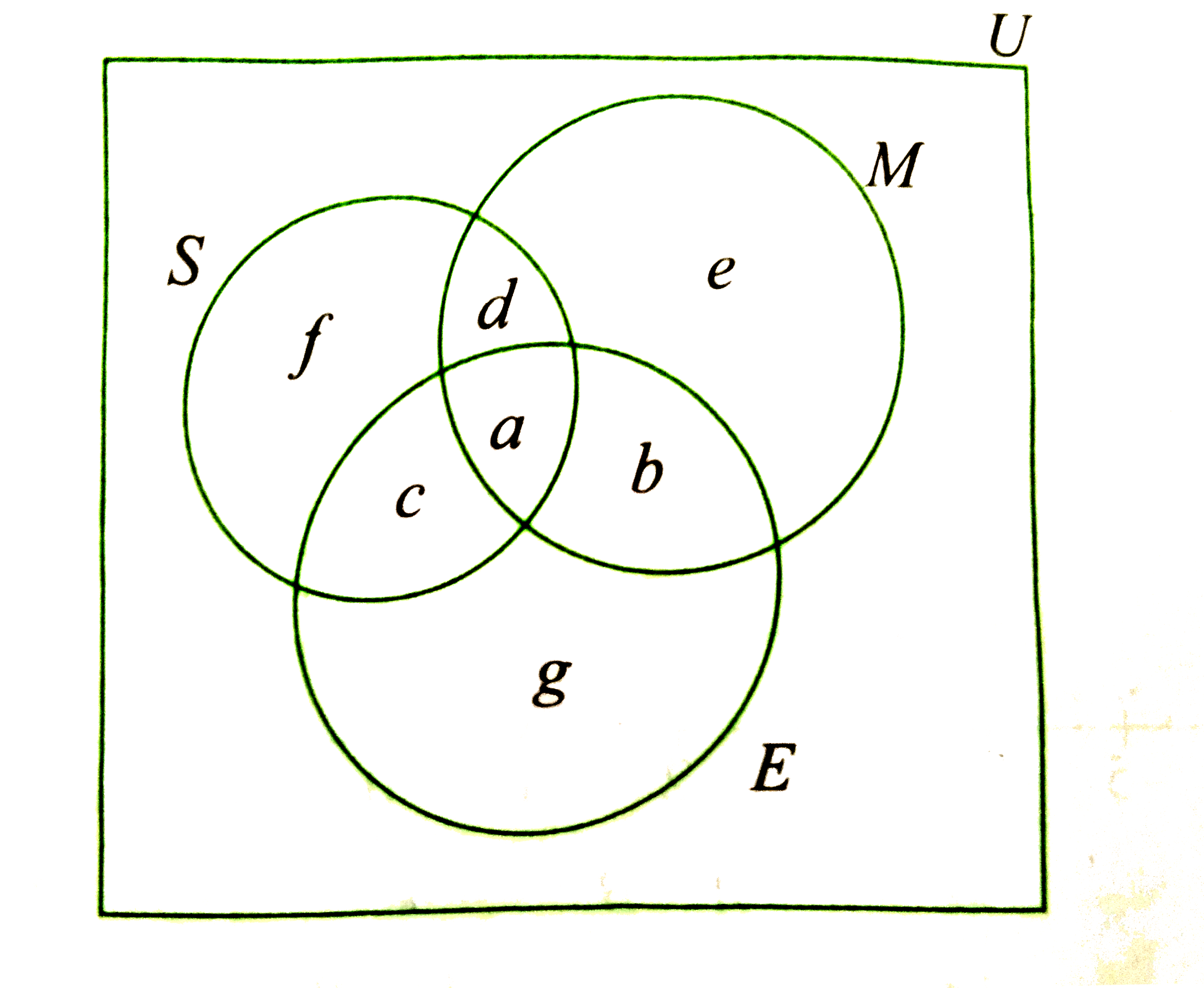
From the Venn diagram , we have
`a= ( E cap M cap S ) = 4 and a+ d = n ( M cap S) = 7 rArr d= 3 `
`a +b =n(M cap E ) =6 " " rArr b= 2`
`a+ c =n( S cap E ) = 4 " " rArr c= 0 `
a+b+ d+ e= n( M)= 12
`rArr 4+2+3+e = 12 " " rArr e= 3`
a+b+c+g = 15
`rArr 4+2+0+g= n( E) = 15 rArr g= 9`
a+c+d+f= n(s)=8
`rArr 4+0+3+f= 8 " " rArr f= 1`
Number of students passed in
(a) English and Mathematics but not in Science = b= 2
( b) Mathematics and Science but not in English = d= 3
Mathmatics only = e= 3
( d) more than one subject =a+b+c+d+= 4+2+0+3=9