If the equation ∣∣x2+bx+c∣∣=k has four real roots, then b2−4c>0and0<k<4c−b24 b2−4c<0and0<k<4c−b24 b2−4c>0andk>4c−b24 none of theseSolution in Tamil
We have ∣∣x2+bx+c∣∣=k
For the equation to have four real roots, the line y=k must intersect y=∣∣x2+bx+c∣∣ at four points, which is not possible if D=0orD<0 as the possible graphas of y=∣∣x2+bx+c∣∣ will be as follows.
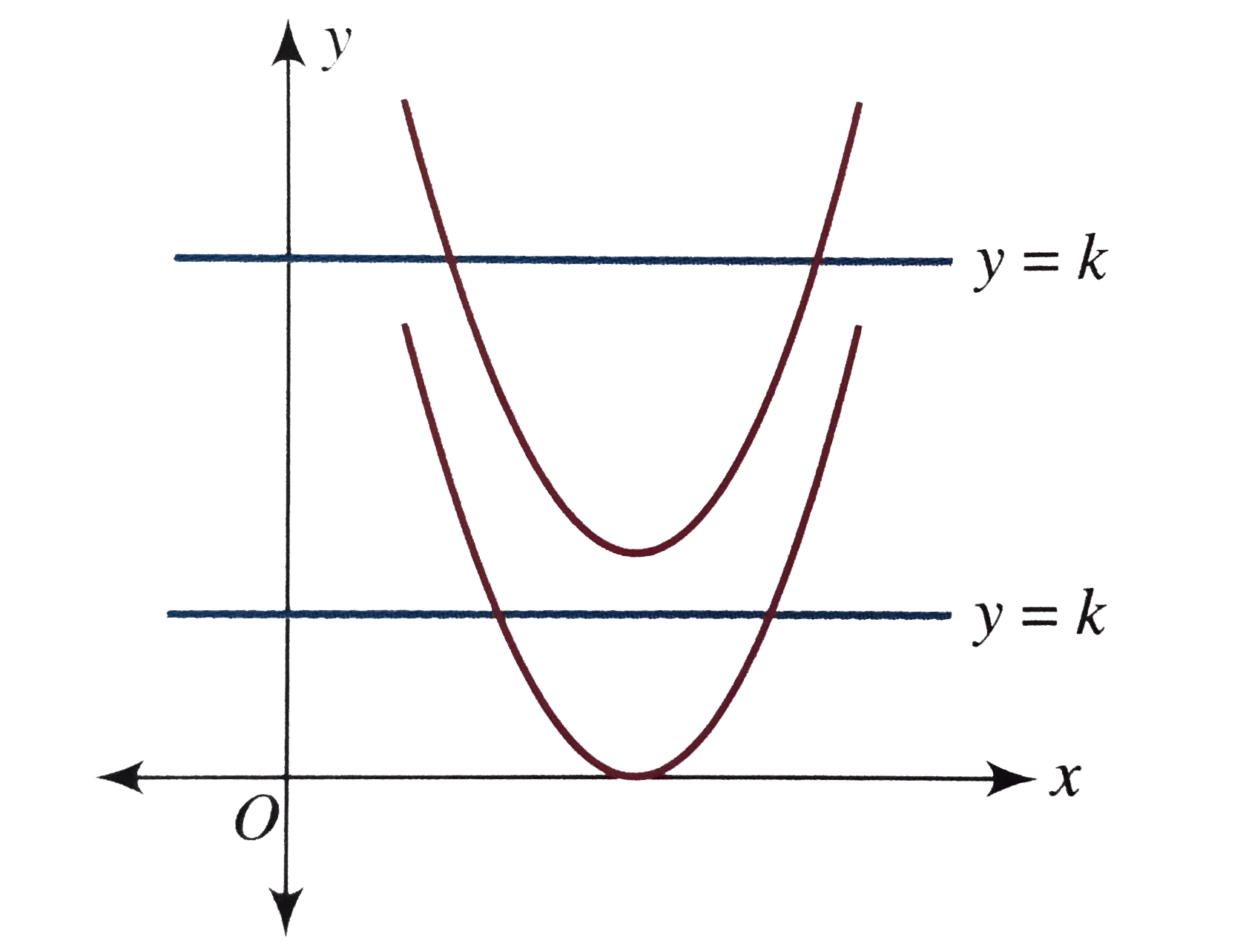
For the above graphs, the equation ∣∣x2+bx+c∣∣=k can have maximum two real roots. So for four real roots, we must have D>0, so the graph of y=x2+bx+c is as follows.
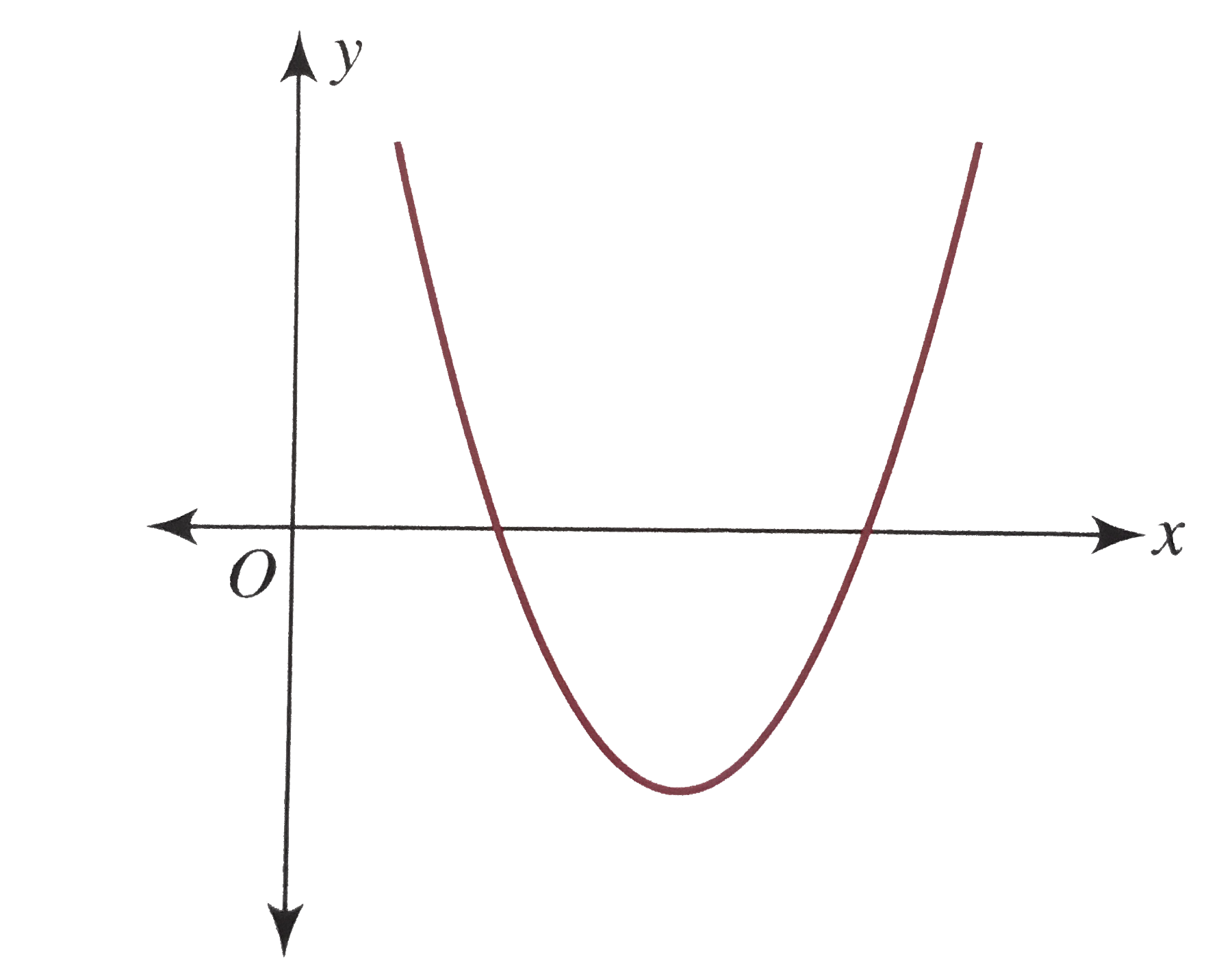
So the graph of y=∣∣x2+bx+c∣∣ will be as follows.

Now the equation ∣∣x2+bx+c∣∣=k will have four real if the line y=k intersects the above graph between the x-axis and point A.
Hence we have 0<k<4c−b24
Also D>0∴b2−4c>0.
Topper's Solved these Questions
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
14 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
Similar Questions
Draw the graph of y=tan−1x−cot−1x.
View SolutionDraw the graph of y=tan−1x+cot−1x
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View Solutiona^(2)+b^(2)+4c^(2)=2a+2b-4c+3=0
View SolutionIf both roots of the equation ax2+x+c−a=0 are imaginary and c>−1, then a.3a>2+4c b.3a<2+4c c.c<a d. none of these
View SolutionIf the equation ∣∣x2+bx+c∣∣=k has four real roots, then
A. b2−4c>0and0<k<4c−b24
B. b2−4c<0and0<k<4c−b24
C.b2−4c>0andk>4c−b24
D. none of these
View Solutiona^(2)-b^(2)-4bc+4c^(2)
View SolutionConsider a circle x2+y2+ax+by+c=0 lying completely in the first quadrant. If m1andm2 are the maximum and minimum values of yx for all ordered pairs (x,y) on the circumference of the circle, then the value of (m1+m2) is (a)a2−4cb2−4c (b) 2abb2−4c (c)2ab4c−b2 (d) 2abb2−4ac
View Solutionb^(2)+c^(2)+2bc+4b+4c
View Solutiona2−b2−4ac+4c2
View SolutionIf the roots of the equation x2−bx+c=0 are two consecutive integers, then find the value of b2−4c
View SolutionIf the equation ∣∣x2+bx+c∣∣=k has four real roots, then
A. b2−4c>0and0<k<4c−b24
B. b2−4c<0and0<k<4c−b24
C.b2−4c>0andk>4c−b24
D. none of these
View SolutionConsider a circle x2+y2+ax+by+c=0 lying completely in the first quadrant. If m1andm2 are the maximum and minimum values of yx for all ordered pairs (x,y) on the circumference of the circle, then the value of (m1+m2) is (a)a2−4cb2−4c (b) 2abb2−4c (c)2ab4c−b2 (d) 2abb2−4ac
View SolutionIf the equation ∣∣x2+bx+c∣∣=k has four real roots, then a. b2−4c>0 and 0<k<4c−b24 b. b2−4c<0 and 0<k<4c−b24 c. b2−4c>0 and k>4c−b24 d. none of these
View SolutionConstruct a quadrilateral ABCD in which AB=6cm, BC=4cm, CD=4cm, ∠B=950and ∠C=900.
View SolutionResolve into factors a^4b^4(a^2-b^2)+b^4c^4(b^2-c^2)+c^4a^4(c^2-a^2)
View Solution
