Discuss the differentiability of f(x)=mim.{|x|,|x−2|,2−|x−1|}.Solution in Tamil
∵f(x)=mim.{|x|,y|x−2|,2−|x−1|}
Draw the graphs of y=|x|,y=|x−2|andy=2−|x−1|.
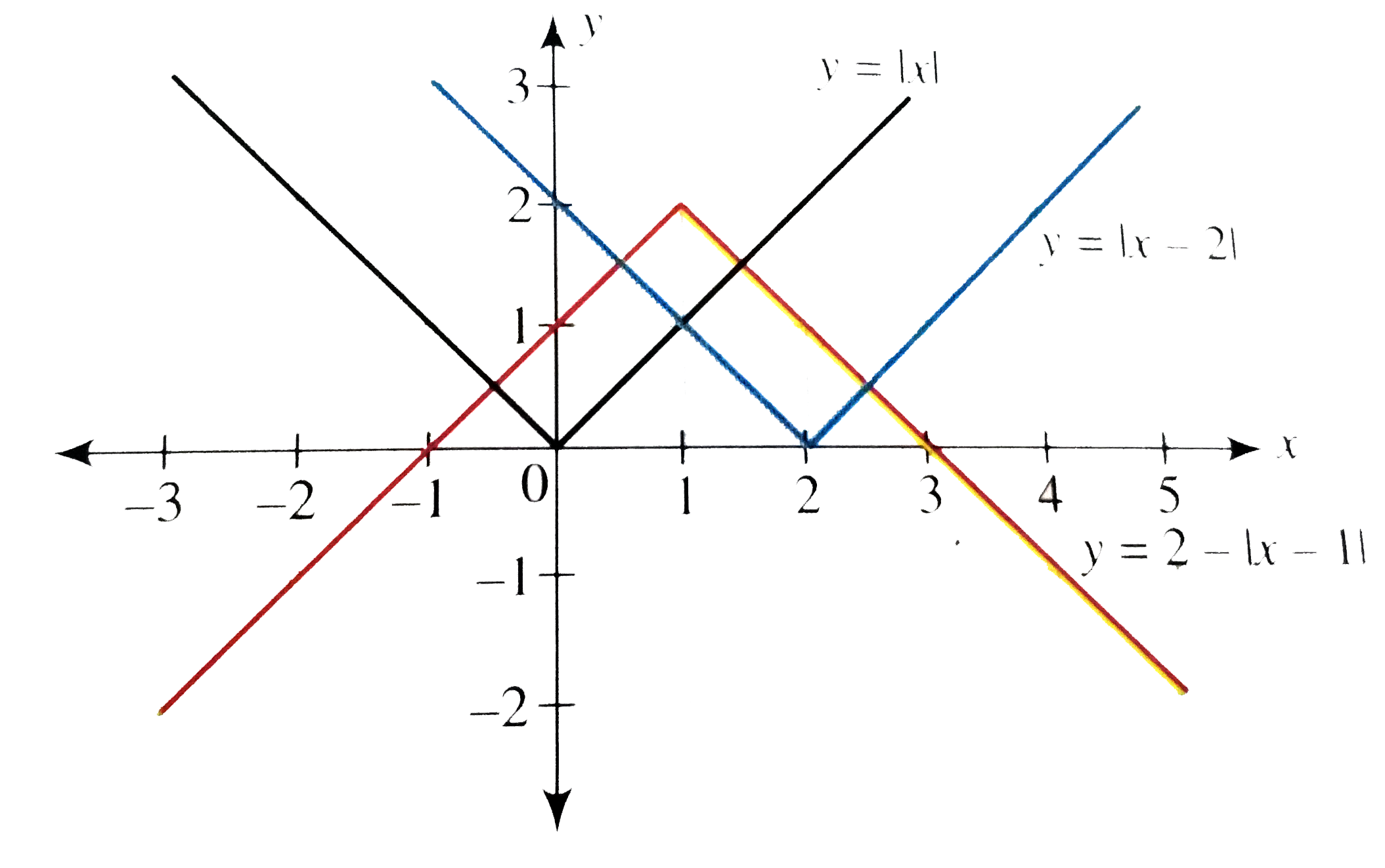
Graph of y=mim.{|x|,|x−2|,2−|x−1|} is as follows.
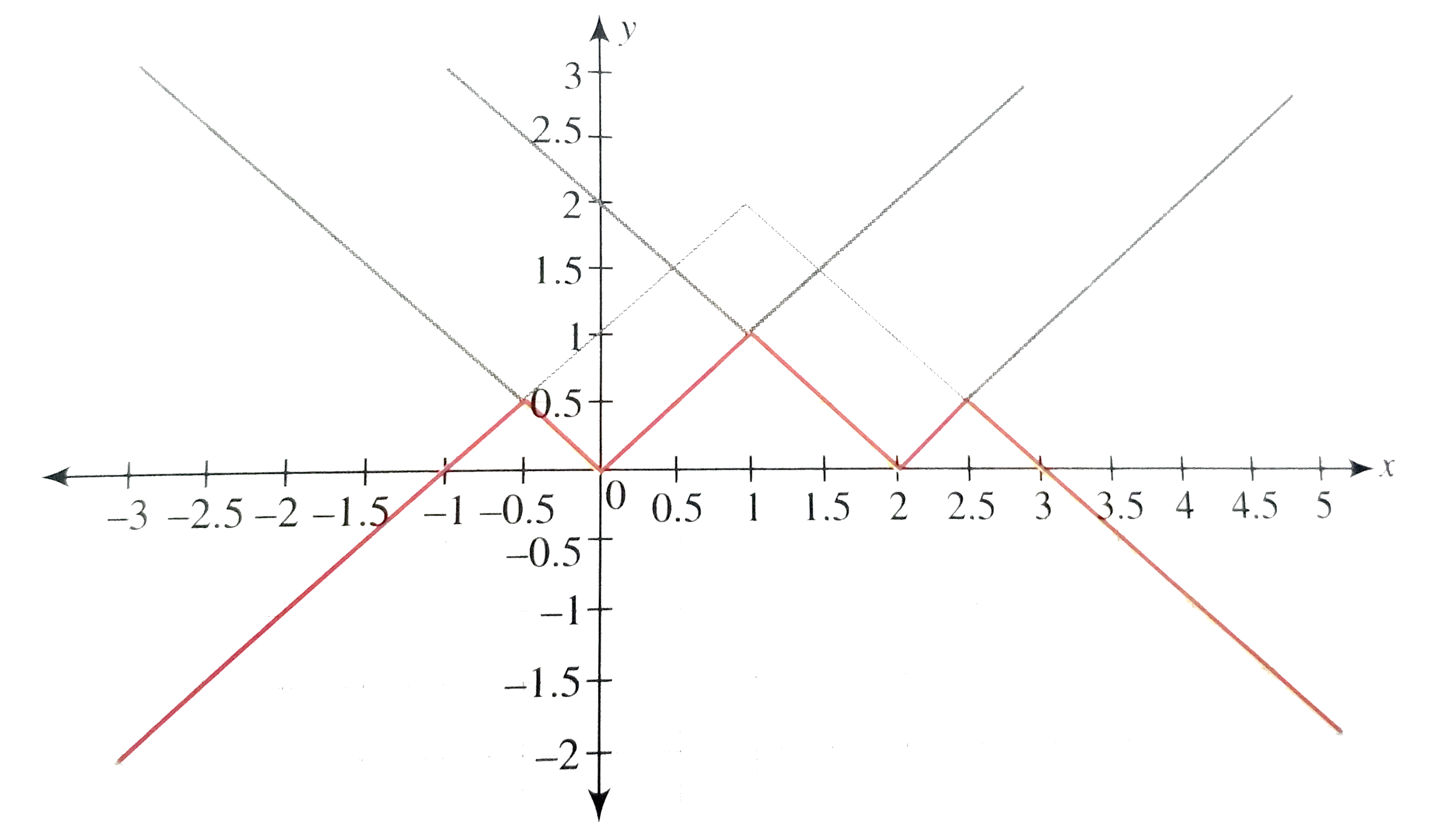
It is clear from the graph that
f(x)=mim.{|x|,|x−2|,2−|x−1|} is continuous AAx inR and non-differentiable at x=−12,0,1,2,52.
Topper's Solved these Questions
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
14 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
Similar Questions
Draw the graph of y=tan−1x−cot−1x.
View SolutionDraw the graph of y=tan−1x+cot−1x
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDiscuss the differentiability of f(x)=|px[x]|,−1<x≤2
View SolutionDiscuss the differentiability of f(x)=arcsin2x1+x2
View SolutionDiscuss the continuity and differentiability of f(x)={1−x, x<1(1−x)(2−x), 1≤x≤23−x, x>2
View SolutionDiscuss the differentiability of f(x)=|x−1|+|x−2|
View SolutionDiscuss the differentiability of f(x)=mim.{|x|,|x−2|,2−|x−1|}.
View SolutionIf f(x)={|x|−|x−1|}2, draw the graph of f(x) and discuss its continuity and differentiability of f(x)
View SolutionDiscuss the differentiability of f(x)=|px[x]|,−1<x≤2
View SolutionDiscuss the differentiability of f(x)=(x2−1)∣∣x2−x−2∣∣+sin(|x|).
View SolutionDiscuss the differentiability of f(x)=mim.{|x|,|x−2|,2−|x−1|}.
View SolutionDiscuss the continuity and differentiability of f(x)={1−x,x<1(1−x)(2−x),1≤x≤2(3−x),x>2
View SolutionDiscuss the continuity and differentiability of f(x)={1−x, x<1 (1−x)(2−x), 1≤x≤2 3−x, x>2
View SolutionDiscuss the differentiability of f(x)=|x−1|+|x−2|
View Solution
