Question

Prove that the equation $2s\in x\left|x\right|+a$
has not solution for $a\in (\frac{3\sqrt{3}-\pi }{3}-\infty )\stackrel{.}{}$

Explanation

`sinx=(1)/(2)|x|+(a)/(2)`
Draw the graphs of `y=2sinxandy=|x|`.

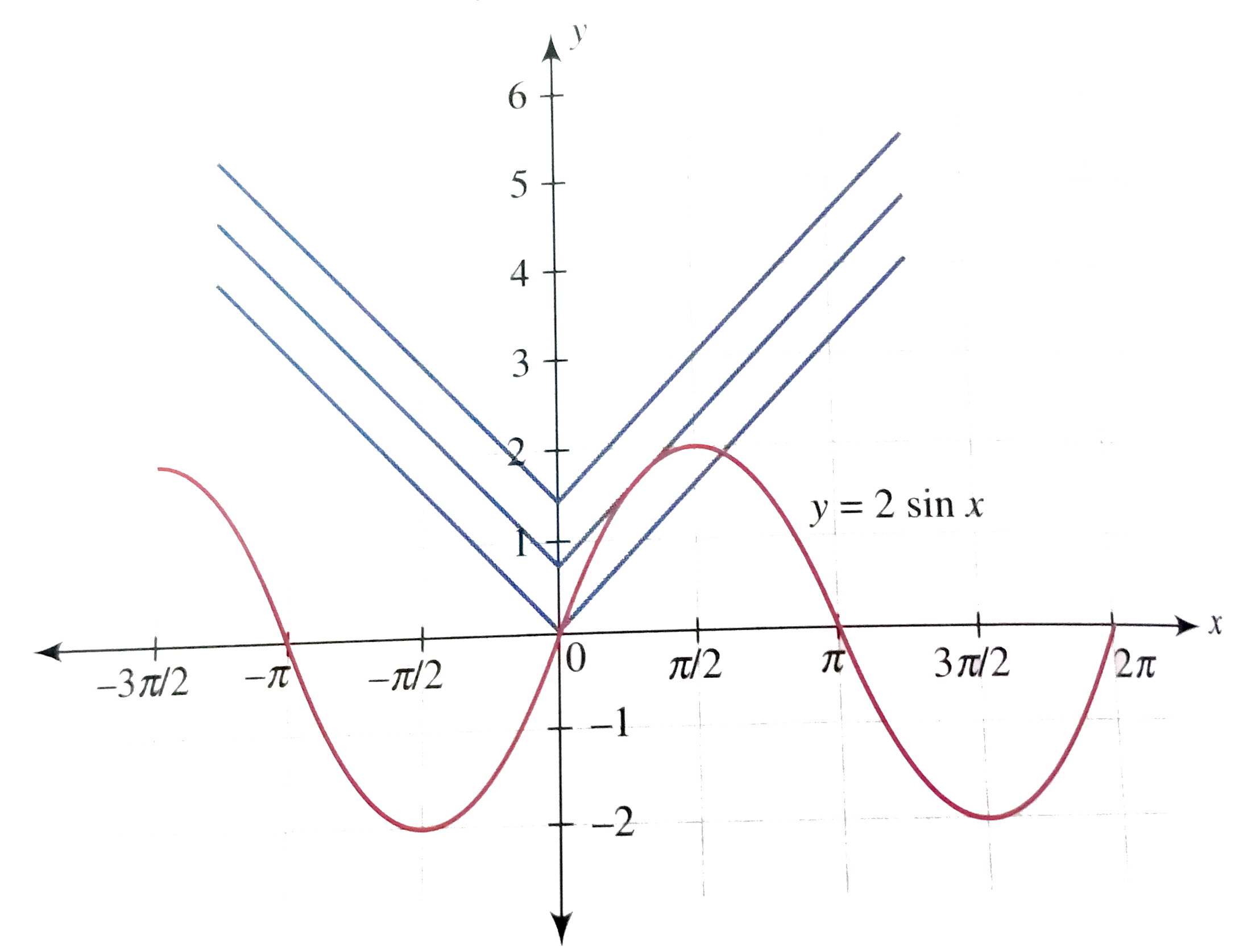
The equation `2sinx=|x|+a` will have a solution so long as the line `y=|x|+a` intersects or at least touches the curve `y=2sinx`. When the graphs touch, we have
`(dy)/(dx)=2cosx=1,impliesx=(pi)/(3)`
Hence for no solution,
`(pi)/(3)+agt2sin""(pi)/(3)`
`impliesagt(3sqrt3-pi)/(3)`