For $a \leq 0,$ jdetermine all real roots of the equation
$x^{2} - 2 a | x - a | - 3 a^{2} = 0$ Solution in Tamil

Video Solution

Text Solution

Verified by Experts

We have $x^{2} - 2 a | x - a | - 3 a^{2} = 0$
$∵ \frac{x^{2} - 3 a^{2}}{2 a} = | x - a |$
Roots of the equation are values of x where the graphs of $∵ \frac{x^{2} - 3 a^{2}}{2 a} and y = | x - | a$ intersect.

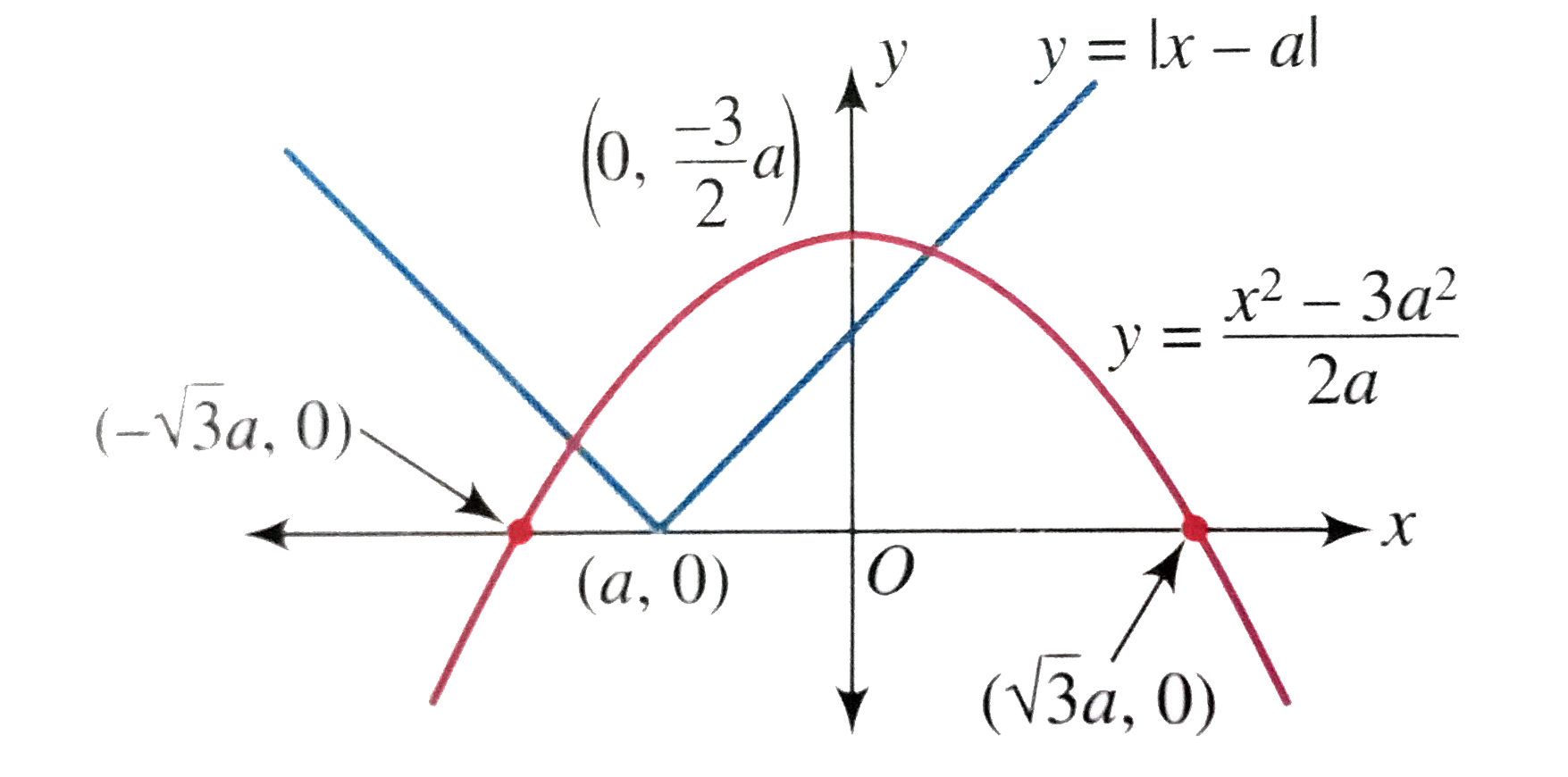
From the graph, we have $\frac{x^{2} - 3 a^{2}}{2 a} = a - x for x < a$
and $\frac{x^{2} - 3 a^{2}}{2 a} = x - a for x > a$
Form (i), $x^{2} - 3 a^{2} = 2 a^{2} - 2 a x$
$\Rightarrow x^{2} + 2 a x - 5 a = 0$
$\Rightarrow x = \frac{- 2 a \pm \sqrt{4} a^{2} + 20 a^{2}}{2}$
$= \frac{- 2 a \pm 2 a \sqrt{6}}{2}$
$= - a + a \sqrt{6} (a s x < a)$
From (ii),
$x^{2} - 2 a (x - a) 3 a^{2} = 0$
$\Rightarrow x^{2} - 2 a x - a^{2} = 0$
$\Rightarrow x = \frac{2 a \pm \sqrt{4} a^{2} + 4 a^{2}}{2} = a - a \sqrt{2} (a s x > a)$
Thus, the solution set is $(- a + a \sqrt{6}, a - a \sqrt{2})$ .

Updated on:21/07/2023

|

Class 12 MATHS LINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

CENGAGE-GRAPHICAL TRANSFORMATIONS-Exercise

Home
Ask Doubt
Profile