A coin is toosed three times consider the following events. A:'No head appears', B: 'Exactly one head appears' and C: 'Atleast two heads appear'.Solution in Tamil
The sample space of the experiment is
S={HHH,HHT,HTH,THH,HTT,THT,TTH,TTT}
A={TTT}
B={HTT,THT,TTH}
C={HHT,HTH,THH,HHH}
Now, A∪B∪C={TTT,HTT,THT,TTH,HHT,HTH,THH,HHH}=S
Therefore, A, B and C are exhaustive events.
Also, A∩B=ϕ,A∩C=ϕandB∩C=ϕ
Therefore, A, B and C form a set of mutually exclusive and exhaustive events.
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Solved Example
1 Videos
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise 9.1
6 Videos
- PROBABILITY AND STATISTICSBOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank
24 Videos
- PROBABILITY IIBOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - JEE Advanced Previous Year
25 Videos
Similar Questions
There are two bags each containing 10 books all having different titles but of the same size. A student draws out books from the first bag as well as from the second bag. Find the probability that the different between the books drawn from the two bags does not exceed 2.
View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
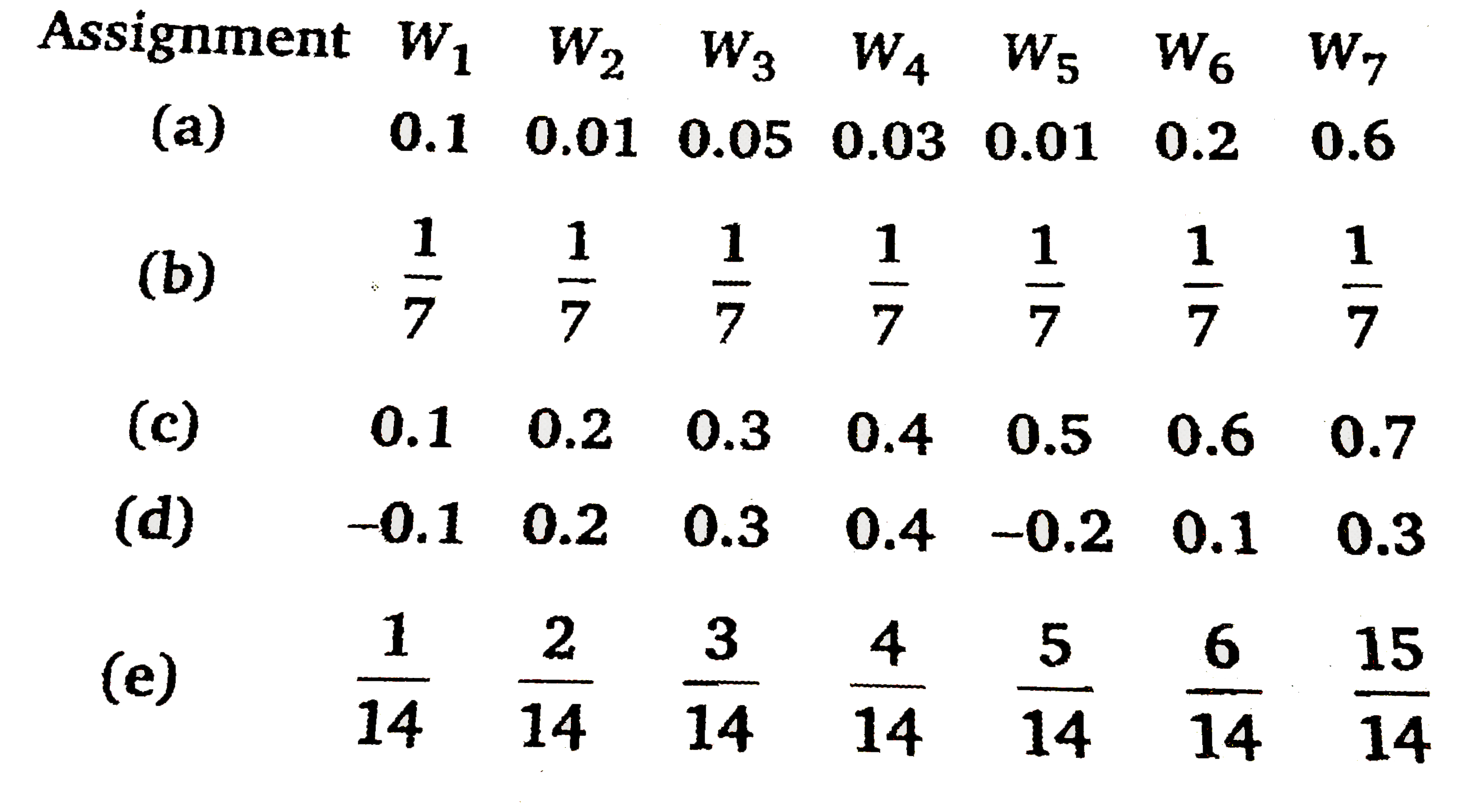
View SolutionIf two events A and B are such that P(Al)=0.3, P(B)=0.4 and P(A∩Bl)=0.5, then P(BA∪Bl) equals
View SolutionA signal which can be green or red with probability 45and15 respectively, is received by station A and then and 3 transmitted to station B. The probability of each station receiving the signal correctly is 34 If the signal received at station B is green, then the probability that the original signal was green is (a) 35 (b) 67 (c) 2023 (d) 920
View SolutionA coin is tossed three times, consider the following events.
A : No head appears,
B: Exactly one head appears’ and
C: Atleast two appear
Do they form a set of mutually exclusive and exhaustive events?
View SolutionThree fair coins are tossed.If both heads and tail appear,then determine the probability that exactly one head appears
View SolutionA coin is tossed three times.
Event A: two heads appear
Event B: last should be head
Then identify whether events A and B are independent or not.
View SolutionIf three coins are tossed simultaneously, then find the probability of the following events :
(i) Event A : No head appears
(ii) Event B : Head appears at least twice
(iii) Event C: Head appears twice.
View SolutionA coin is tossed three times. Given that at least one head appears, what is the probability that exactly two heads will appear?
View SolutionA coin is toosed three times consider the following events. A:'No head appears', B: 'Exactly one head appears' and C: 'Atleast two heads appear'.
View SolutionA coin is toosed three times consider the following events. A:'No head appears', B: 'Exactly one head appears' and C: 'Atleast two heads appear'.
View SolutionA coin is toosed three times consider the following events. A:'No head appears', B: 'Exactly one head appears' and C: 'Atleast two heads appear'.
View SolutionA coin is toosed three times consider the following events. A:'No head appears', B: 'Exactly one head appears' and C: 'Atleast two heads appear'.
View SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
View SolutionA coin is tossed three times.
Event A: two heads appear
Event B: last should be head
Then identify whether events A and B are independent or not.
View SolutionA coin is tossed three times, consider the following events.
A : 'No head appears,
B : 'Exactly one head appears' and
C: 'At least two heads appear'.
Do they form a set of mutually exclusive and exhaustive events?
View Solution
