If a vertex of a triangle is (1,1) , and the middle points of two sides passing through it are −2,3) and (5,2), then find the centroid and the incenter of the triangle.Solution in Tamil
Let E and F be the midpoints of AB and AC. Let the coordinates of B and C be (α,β) and (γ,δ) respectively. Then −2=1+α2,3=1+β2,
5=1+γ2,2=1+δ2
∴α=−5,β=5,γ=9,δ=3
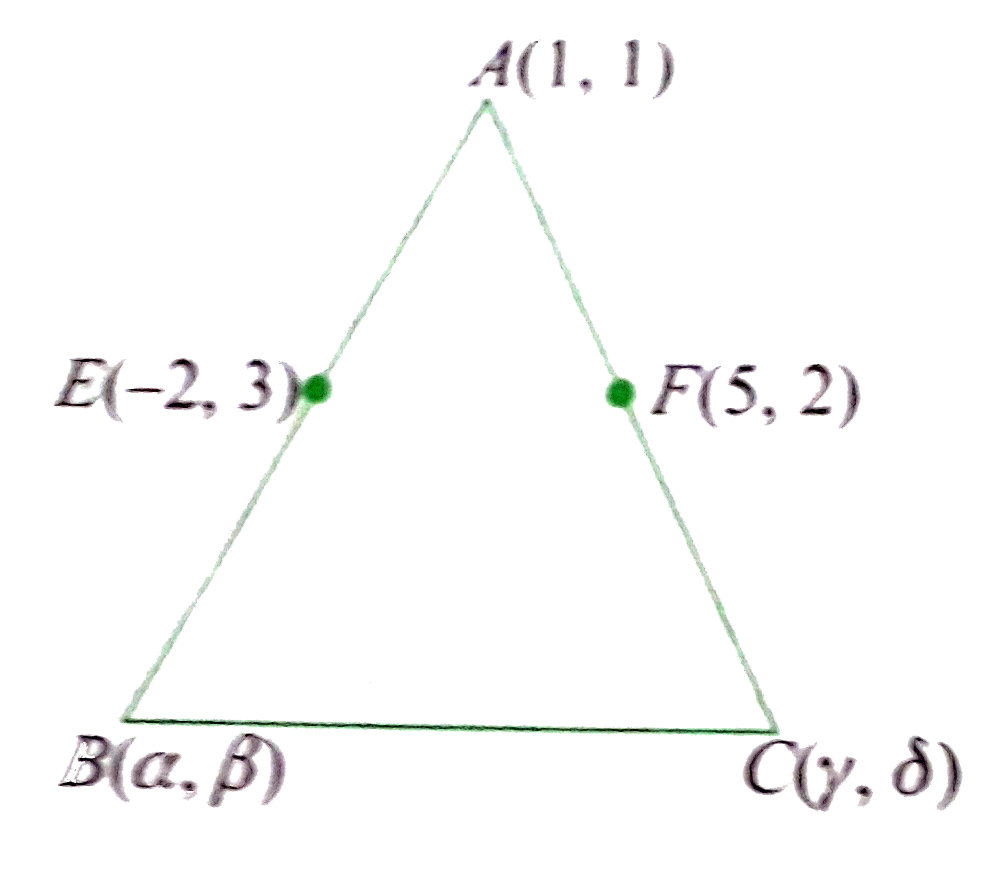
Therefore, the coordinates of B and C are (−5,5) and (9,3), respectively.
Then the centroid is
(1−5+93,1+5+93)≡(53,3)
and a=BC=√(−5−9)2+(5−3)2=10√2
b=CA=√(9−1)2+(3−1)2=2√17
c=AB=√(1+5)2+(1−5)2=2√13
Then, the incenter is
(10√2(1)+2√17(−5)+2√13(9)10√2+2√17+2√13,10√2(1)+2√17(5)+2√13(3)10√2+2√17+2√13)
i.e., (5√2−5√17+9√135√2+√17+√13,5√2+5√17+3√135√2+√17+√13)
Similar Questions
If a vertex of a triangle is (1,1) , and the middle points of two sides passing through it are −2,3) and (5,2), then find the centroid of the triangle.
04:24View SolutionIf the middle points of the sides of a triangle are (−2,3),(4,−3),and(4,5) , then find the centroid of the triangle.
02:38View SolutionIf a vertex of a triangle is (1,1) , and the middle points of two sides passing through it are −2,3) and (5,2), then find the centroid and the incenter of the triangle.
14:29View Solutionif a vertex of a triangle be(1,1) and the middle point of the sides through this point are(-2,3) and (5,2) , find the other vertices
03:50View SolutionA triangle having a vertex as (1,2) has mid-point of sides passig from this vertex as (−1,1) and (2,3) thent he centroid of the triangle is
05:30View SolutionIf the middle points of the sides of a triangle are (−2,3),(4,−3),and(4,5) , then find the centroid of the triangle.
02:24View SolutionIf a vertex of a triangle is (1,1) , and the middle points of two sides passing through it are -2,3) and (5,2), then find the centroid of the triangle.
05:03View Solution
