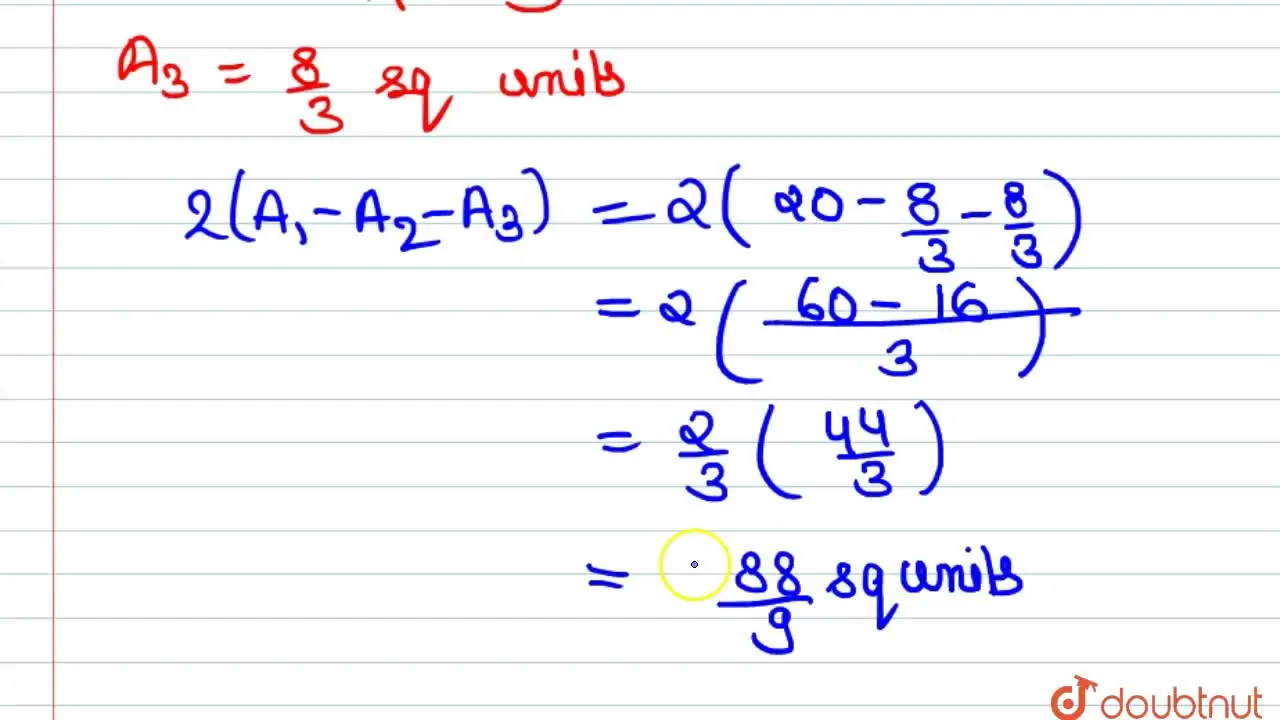The area bounded by 4y=∣∣4−x2∣∣ and y=7−|x| in square units is equal to…
Step by step video & image solution for The area bounded by 4y=|4-x^2| and y=7-|x| in square units is equal to… by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
The area bounded by y=4−x2,y=0 and y = 3 is
View SolutionThe area bounded by y2=4xandy=2x−4 is
View SolutionThe area bounded by y2=4xandy=2x−4 is
View SolutionThe area (in sq. units) bounded by y=4x−x2 and y=xis
View SolutionThe area bounded by the curve y=4−x2 and X-axis is
View SolutionA curve y = (x) which passes through (4,0) satisfy the differential equation xdy+2ydx=x(x−3)dx . The area bounded by y=f(x) and line y=x (in square unit) is- 32 (2) 643 (3) 1283 (4) 64
View SolutionThe area bounded by y+x2≤4x and y≥3 is k sq. units, then 3k is equal to
View SolutionThe area of the figure bounded by |y|=1−x2 is in square units,
View SolutionFind the area of the region bounded by 4y=∣∣4−x2∣∣ and y=7−|x|
View SolutionThe maximum area bounded by the curves y2=4ax,y=ax and y=xa,1≤a≤2 in square units is equal to….
View Solution