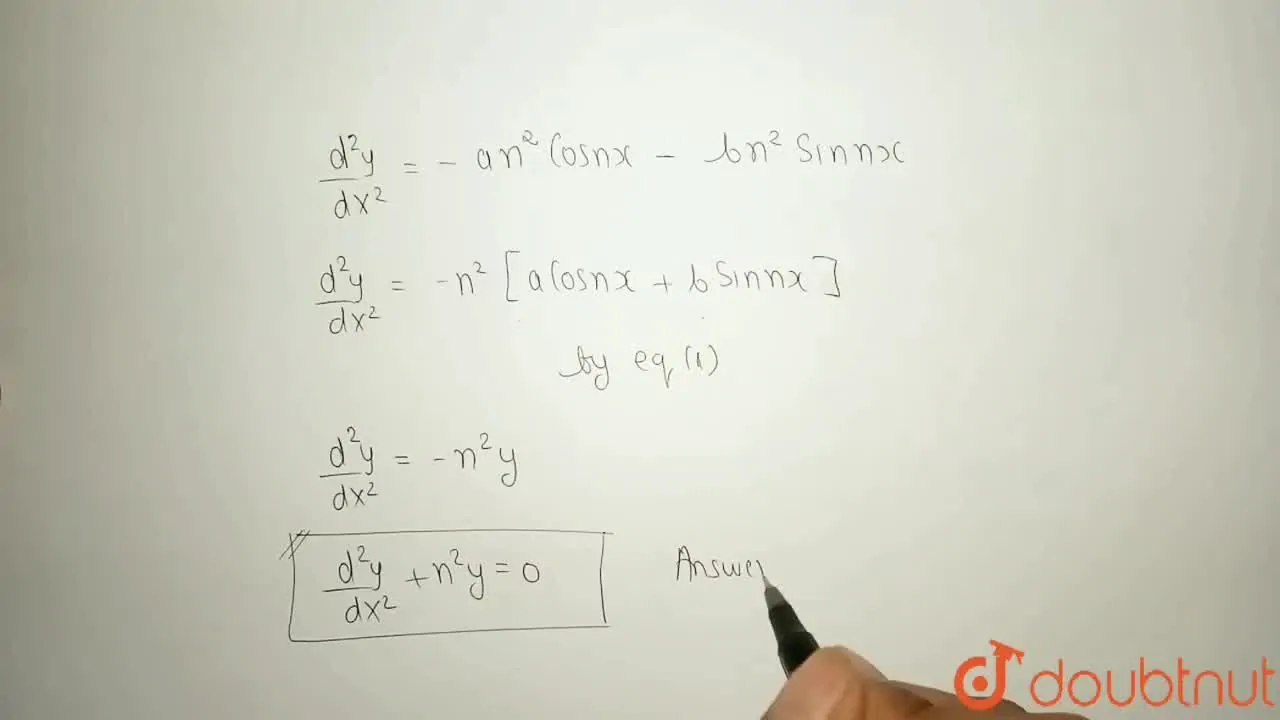if a, b are arbitrary constants, find the differential equation of y=acosnx+bsinnx
Step by step video & image solution for if a, b are arbitrary constants, find the differential equation of y=acosnx+bsinnx by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
If a is arbitrary constant, find the differential equation of x2+y2=a2
View SolutionIf a and b are arbitrary constants, then find the differential equation corresponding to y=acos(x+b).
View SolutionIf A and B are arbitrary constants, then find the differential equation corresponding to the equation y=Ax+B.
View SolutionThe general solution of a differential equation is y=aebx+c where are arbitrary constants. The order the differential equation is :
View SolutionIf y=Asin(θ+B), where A and B are arbitrary constant then to form a differential equation how many times it should be differentiated ?
View SolutionFor all values of A and B, find the differential equation of y=Acospx+Bsinpx.
View SolutionIf a and b are arbitrary constants, then the order and degree of the differential equation of the family of curves ax2+by2=2 respectively are
View SolutionFor all values of A and B, find the differential equation of y=Asinx+Bcosx.
View SolutionThe number of arbitrary constants in the particular solution of a differential equation of third order are:
(A) 3 (B) 2 (C) 1 (D) 0View SolutionThe number of arbitrary constants in the particular solution of a differential equation of third order are: (A) 3 (B) 2 (C) 1 (D) 0
View Solution